-
Ecuación de la fuerza, periodo, velocidad máxima y energía mecánica de un oscilador armónico (7783)
Una partícula de 10.0 g experimenta un MAS con una amplitud de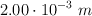 
y una aceleración máxima de magnitud 
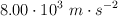. La constante de fase es 
.
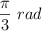a) Escribe una ecuación para encontrar la fuerza sobre la partícula como función del tiempo.
b) ¿Cuál es el periodo del movimiento?
c) ¿Cuál es la máxima rapidez de la partícula?
d) ¿Cuál es la energía mecánica total de este oscilador armónico simple?
-
Movimiento vibratorio en una cuerda tensa (7779)
Un extremo de una cuerda tensa horizontal de 3 m de longitud está sometida a un movimiento vibratorio armónico simple. En el instante t = 4 s la elongación de ese punto es de 2 cm. Se comprueba que la onda tarda 0.9 s en llegar de un extremo a otro de la cuerda y que la longitud de onda es de 1 m. Calcula:
a) La amplitud del movimiento ondulatorio.
b) La velocidad de vibración en el punto medio de la cuerda para t = 1 s.
-
Ecuación de la velocidad de una masa que vibra en un resorte (7522)
Una masa de 150 g está unida a un resorte de constante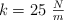 
. La amplitud de la oscilación es 5 cm, ¿cuál es la ecuación de la velocidad, expresada en m/s, suponiendo que el desfase es cero?
-
Velocidad de un oscilador cuando pasa por la posición de equilibrio (7080)
Un cuerpo efectúa un MAS y en el punto correspondiente a su elongación máxima, que es de 9 cm, la aceleración es de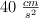 
. Calcula el valor de la velocidad cuando el cuerpo pasa por la posición de equilibrio.
-
Velocidad, amplitud y frecuencia de un oscilador armónico a partir de su ecuación de la posición
La ecuación del movimiento de una partícula (en unidades SI) viene dada por:
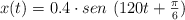
a) ¿Cuál es la ecuación de la velocidad?
b) ¿Cuáles son las condiciones iniciales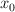 
y 
?
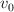c) ¿Cuáles son la amplitud y la frecuencia del movimiento?
Velocidad
Ejercicios FyQ