-
Frecuencia de oscilación de un cuerpo colgado de un resorte (7523)
Un cuerpo de 300 g se encuentra unido al techo a través de un muelle. El peso del cuerpo hace que el muelle se deforme 4 cm, calcula la frecuencia de oscilación del cuerpo cuando se desplaza de su posición de equilibrio.
-
Frecuencia, y ecuación del movimiento de un muelle que oscila (6564)
Al colocar un bloque de 2 kg suspendido de un muelle se produce un alargamiento de 4 cm. Si a continuación se le estira 5 cm y se suelta dejándolo oscilar libremente, el bloque describe un MAS. Calcula:
a) La constante recuperadora del muelle.
b) La frecuencia de las oscilaciones.
c) La ecuación del movimiento.
-
Velocidad, amplitud y frecuencia de un oscilador armónico a partir de su ecuación de la posición
La ecuación del movimiento de una partícula (en unidades SI) viene dada por:
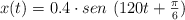
a) ¿Cuál es la ecuación de la velocidad?
b) ¿Cuáles son las condiciones iniciales 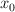 y
y 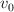 ?
?
c) ¿Cuáles son la amplitud y la frecuencia del movimiento?
-
Análisis del movimiento armónico simple de un partícula (6535)
Una partícula que se mueve describiendo un MAS durante un tiempo de 18 s. Tiene la siguiente ecuación (en unidades SI):
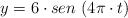
a) Halla el periodo del movimiento.
b) Halla la frecuencia.
c) Halla la elongación (x).
d) Halla el valor de la aceleración.
e) Si duplica el tiempo que tarda para dar una oscilación completa, ¿qué sucede con la elongación?
f) Si cuadruplico el valor de la masa que está oscilando, ¿qué pasa con la velocidad?
-
Periodo, frecuencia y frecuencia angular en un movimiento armónico simple (6472)
Si una partícula da 5 oscilaciones en 10 segundos, halla:
a) Su periodo.
b) Su frecuencia.
c) Su velocidad angular.
 Frecuencia
Frecuencia