-
Fuerza máxima sobre un cuerpo que oscila armónicamente (7782)
Un pequeño cuerpo de 0.12 kg de masa experimenta un MAS de una amplitud de 8.50 cm y un período de 0.20 s.
a) ¿Cuál es la magnitud de la fuerza máxima que actúa sobre él?
b) Si las oscilaciones las produce un resorte, ¿cuál es la constante del resorte?
-
Longitud y ángulo máximo de un péndulo (7668)
Un reloj de péndulo está construido de forma que el período coincide exactamente con 1 s y la amplitud de su movimiento es 5 cm, definidos en la proyección horizontal. Si lo aproximamos a un péndulo ideal como una masa de 1.5 kg colgada de una barra sin masa de longitud L y sin rozamiento:
a) Calcula la longitud de la barra y el ángulo máximo con el que oscila el péndulo.
b) Escribe la ecuación de la aceleración si sabemos que el movimiento comienza cuando la elongación es cero y determina el valor de la fuerza recuperadora en el instante 1.3 s.
-
Frecuencia de oscilación de un cuerpo colgado de un resorte (7523)
Un cuerpo de 300 g se encuentra unido al techo a través de un muelle. El peso del cuerpo hace que el muelle se deforme 4 cm, calcula la frecuencia de oscilación del cuerpo cuando se desplaza de su posición de equilibrio.
-
Constante elástica efectiva de dos resortes en serie (7078)
¿Cuál es el valor de la constante efectiva de dos resortes idénticos conectados en serie que está utilizando un artista para una instalación de la próxima bienal, si la constante de cada uno de ellos es de 200 N/m y sobre los cuales cuelga un determinado peso?
-
Constante de un resorte y fuerza recuperadora para una elongación (7073)
La velocidad máxima de una masa de 100 g atada a un resorte es de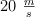 
, siguiendo un MAS. Si su amplitud es de 50 cm:
a) ¿Cuál es el valor de la constante k?
b) ¿Cuál es la fuerza de restitución a 40 cm de la posición de equilibrio?
Constante recuperadora
Ejercicios FyQ