-
Lanzamiento parabólico en un partido entre Brasil y Argentina (6389)
En un partido amistoso de fútbol entre Argentina y Brasil, cuando estaban empatados a uno y en el minuto 90, el árbitro pita una falta a favor de Brasil alejada 32 m de la portería. El jugador que la lanza es capaz de imprimir una velocidad de 30 m/s a la pelota y la barrera de los jugadores argentinos, de una altura media de 1.80 m, se sitúa a 12 m del punto de lanzamiento. Determina:
a) ¿Cuál debe ser el ángulo del lanzamiento para colocar el balón en la esquina superior izquierda sin que la barrera obstruya el lanzamiento?
b) ¿Cuál debe ser el ángulo del lanzamiento para colocar el balón en la esquina inferior izquierda sin que la barrera obstruya el lanzamiento?
-
Velocidad mínima de un motociclista para saltar un obstáculo (8279)
Calcula la mínima velocidad que debe llevar un motociclista para lograr saltar un obstáculo en su camino que tiene 20 m de largo, si salta con un ángulo de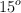 
.
-
Composición de movimientos: velocidad de un remero y velocidad de la corriente (8070)
Un remero entrena en un río que tiene una corriente estable de 0.2 m/s. Realiza un recorrido entre dos embarcaderos ubicados sobre la misma orilla del río, remando aguas abajo, es decir, en el sentido en que fluye la corriente del río. El remero es capaz de remar a una velocidad de 1.8 m/s con respecto al agua quieta. Si el bote demora 15 minutos en llegar al segundo embarcadero, determina la distancia entre ambos embarcaderos.
-
Tiempo mínimo que necesita un coche con aceleración máxima para recorrer un tramo (7851)
Un automóvil debe recorrer 240 m en el menor tiempo posible partiendo con una velocidad de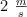 
. Si la máxima velocidad del auto es de 
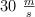y los cambios de marcha le permiten acelerar sin sobrepasar los 
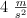. Determina el tiempo mínimo que utilizará en recorrer dicho tramo.
-
Alcance de un proyectil que es disparado sobre un plano inclinado (7837)
Un proyectil es lanzado con una velocidad inicial de 10 m/s, que forma un ángulo de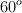 
con la horizontal, contra un plano inclinado que forma 
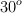con la horizontal. Calcula el alcance, expresado en metros, sobre el plano inclinado.
Considera: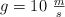 
Composición movimientos
Ejercicios FyQ