-
Ecuación que permite calcular la fuerza necesaria para que una escalera esté en equilibrio sobre la pared (7574)
Una escalera de peso W y longitud L se apoya sobre una pared sin rozamiento. Sobre la escalera se encuentra una persona de peso P, a una distancia S del pie de la escalera, medida a lo largo de esta. El pie de la escalera se encuentra a una distancia D de la esquina inferior de la pared. Determina una expresión para la fuerza que la pared ejerce sobre la escalera, considerando que el sistema se encuentra en equilibrio estático.
-
Momento necesario para girar una ventana (7540)
Calcula el momento de fuerza que se requiere para girar una ventana de 50 cm de ancho y una fuerza de 35 N.
-
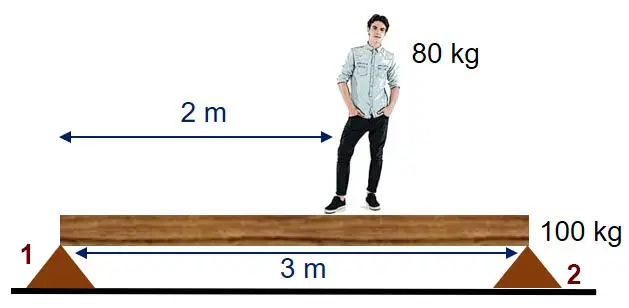
Fuerza que hacen los soportes de una viga que sujeta a una persona (7371)
La viga rígida de 3.0 m de largo y 100 kg de la figura se apoya en cada extremo. Un estudiante de 80 kg se para a 2.0 m del soporte 1. ¿Cuánta fuerza hacia arriba ejerce cada soporte?
Momento de una fuerza
-
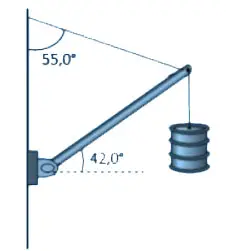
Valor de la tensión para que un pivote permanezca en equilibrio (7345)
Una barra ingrávida esta suspendida sobre un pivote tal como muestra la figura. Si el cilindro que suspende en el extremo de la barra tiene un peso de 600 N:
a) Dibuja el diagrama del cuerpo libre de la barra.
b) Escribe las ecuaciones de las condición de equilibrio.
c) Calcula la magnitud de tensión oblicua.
Momento de una fuerza
-
Refuerzo: Torque o momento de la fuerza aplicada al brazo de una palanca (6938)
Valiéndose de una palanca, un hombre levanta un cuerpo aplicando una fuerza de 200 N a 1.5 m del centro de apoyo o fulcro. Calcula el torque o momento de la fuerza.
 Momento de una fuerza
Momento de una fuerza