Velocidad

(197) ejercicios de Velocidad

(#8457) Seleccionar

Velocidad y aceleración de un móvil en función del tiempo (8457)

Un móvil describe una trayectoria en el plano XY dada por el vector de posición, expresado en unidades SI:

$\vec{r}(t) = (3t^2 - 2)\ \vec{i} + (4 \sen\ 2t)\ \vec{j}$

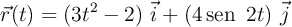
a) Determina los vectores velocidad y aceleración en función del tiempo.

b) Calcula los vectores velocidad y aceleración en el instante 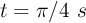$t = \pi/4\ s$ .

c) Halla el módulo de la velocidad y de la aceleración en 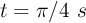$t = \pi/4\ s$ .
(#8224) Seleccionar

Ecuación de la posición, espacio recorrido y velocidad media de un sistema en movimiento (8224)

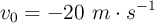Una partícula se mueve a lo largo del eje OX de un sistema de coordenadas con aceleración constante. En el instante inicial pasa por la posición $x_0 = -10\ m$ con una velocidad $v_0 = -20\ m\cdot s^{-1}$ y en t = 3 s su posición es 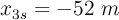$x_{3s} = -52\ m$ . Determina:

a) La ecuación de la posición de la partícula en función del tiempo.

b) El espacio recorrido por la partícula entre t = 3 s y t = 6 s.

c) La velocidad media entre t = 4 s y t = 7 s.

d) Los intervalos de tiempo en que la partícula se aleja del origen.
(#8098) Seleccionar

Velocidad media de un ciclista y tiempo para subir una pendiente (8098)

Un ciclista sube una pendiente con MRU a razon de 10 km/h y la desciende a razón de 15 km/h, empleando 8 horas. ¿En cuanto disminuira el tiempo de subida si su rapidez se incrementa en 2 km/h?
(#7894) Seleccionar

Cinemática: ecuación de la posición en función del tiempo (7894)

Un punto material se mueve según la ecuación horaria: 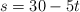$s = 30 - 5t$ (SI). Calcula:

a) Su posición inicial.

b) Su velocidad.

c) Su posición en el instante 3 s.
(#6971) Seleccionar

Velocidad de una bala a partir de un dispositivo rotacional (6971)

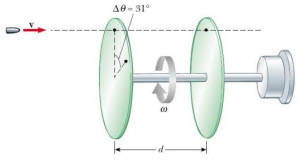
La rapidez de una bala en movimiento puede determinarse al permitir que esta atraviese dos discos giratorios de papel montados sobre un mismo eje y separados por una distancia (d). A partir del desplazamiento angular (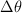 $\Delta \theta$ ) de los agujeros de la bala en los discos y de la rapidez rotacional ( 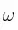$\omega$ ) se puede determinar la rapidez (v) de la bala.

a) Escribe la ecuación para calcular v.

b) ¿Cuál es la velocidad si d = 80 cm, 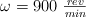$\omega = 900\ \textstyle{rev\over min}$ y $\Delta \theta = 31^0$ ?

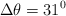Velocidad