Ejercicios FyQ
Una resistencia de 
se conecta a los polos de una pila de fuerza electromotriz 
. Si la resistencia se reemplaza por otra de 
la intensidad de la corriente se duplica. Calcula la resistencia interna de la pila.
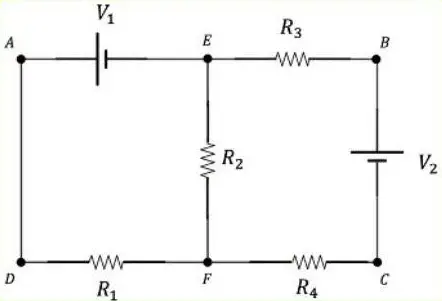
Considera el circuito de la figura donde las resistencias son 
, 
, 
y 
. Las fuentes de voltaje son 
y 
:
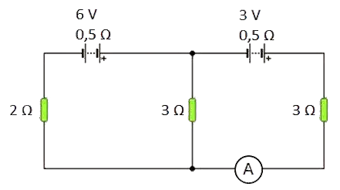
a) Aplica la primera ley de Kirchhoff y escribe la ecuación de las corrientes para el nodo F.
b) Aplica la segunda ley de Kichhoff a la malla EFCBE y encuentra la ecuación correspondiente a las diferencias de potencial.
c) Aplica la segunda ley de Kichhoff a la malla EADFE y encuentra la ecuación correspondiente a las diferencias de potencial.
d) Calcula el valor de la corriente que fluye en la resistencia ubicada entre E y F.
Calcula la resistencia interna de un voltímetro que puede medir hasta 70 V de tensión y soporta una intensidad de corriente máxima de 20 mA.
Se tiene un conductor cuya resistividad es de 
de 40 cm de longitud y sección transversal 
cuando está sometido a una diferencia de potencial de 120 V durante un cuarto de hora. Calcula:
a) La cantidad de calor que desprende.
b) La energía eléctrica expresada en 
.
La chispa de un relámpago artificial de 10 MV libera energía de 
. ¿Cuántos culombios de carga fluyen?
¿Cuál es la carga eléctrica por unidad de tiempo que pasa por una bombilla eléctrica ordinaria de 150 W cuando está conectada a 115 V? ¿A cuántos electrones equivale?
Cuatro resistencias en serie de 220 
se conectan en serie con una batería de 5 V, calcula:
a) La resistencia total.
b) La corriente a través del circuito.
c) Las caídas de voltaje las resistencias.
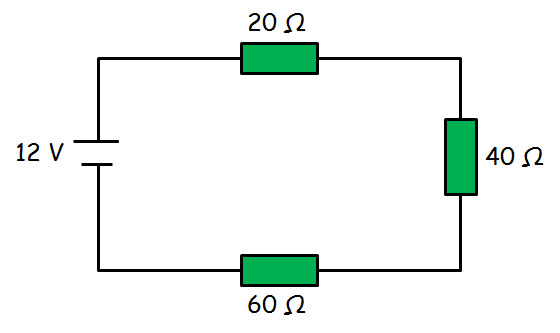
Halla el valor de la resistencia total del circuito mostrado en la figura, el valor de la intensidad de corriente suministrada por la pila, así como los voltajes en cada una de las resistencias:
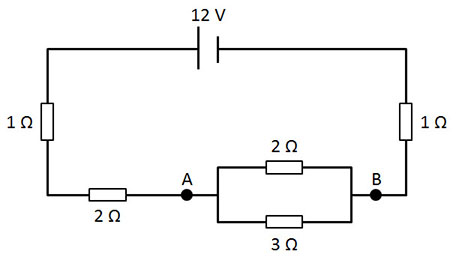
Determina la intensidad que circula por el circuito de la figura , así como la diferencia de potencial entre los puntos A y B:
