Ejercicios Resueltos de Cinemática, dinámica y estática

¿Cuál es el valor de la constante efectiva de dos resortes idénticos conectados en serie que está utilizando un artista para una instalación de la próxima bienal, si la constante de cada uno de ellos es de 200 N/m y sobre los cuales cuelga un determinado peso?

Un objeto es lanzado con velocidad inicial y ángulo con la horizontal de . Calcula la diferencia aproximada entre el alcance en el modelo ideal y el alcance en el modelo con resistencia, suponiendo que b = 0.1.

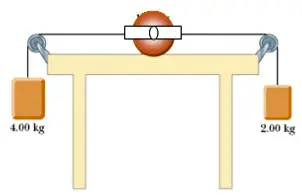
En la figura se muestra un sistema conformado por dos masas colgantes , , dos poleas de radio y masa fijadas en los extremos de la mesa y un disco de radio y masa . Los tres objetos se unen mediante una cuerda que pasa sin deslizarse por las poleas, cuyos ejes carecen de fricción, y se unen al disco por medio de un eje central que le permite rodar libremente sobre una mesa con superficie rugosa. Si el sistema se libera a partir del reposo, halla lo siguiente:

a) El valor de la aceleración del centro de masa del disco.

b) El valor de la rapidez final que alcanza la si recorre 1 m sobre la mesa.

c) El valor de todas las tensiones del sistema.

El siguiente sistema está compuesto por tres masas de igual valor . La constante de recuperación del muelle es . El cuerpo tiene coeficientes de fricción con el suelo y .

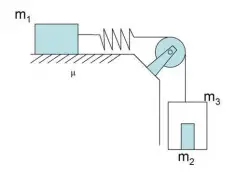
a) Si el sistema se encuentra en reposo: calcula la fuerza de fricción y la longitud que se estira el muelle.

b) Si el sistema se encuentra en movimiento: calcula la fuerza de contacto entre y .

Una esfera sólida de latón, cuyo módulo volumétrico es de , con un diámetro de 3.00 m, es lanzada al océano. ¿Cuánto disminuye el diámetro de la esfera cuando se sumerge a una profundidad de 1.00 km?

Densidad del agua salada:

Una partícula se mueve a lo largo de una recta. Su aceleración está dada por . Encuentra la relación entre la velocidad y el desplazamiento suponiendo que y .

Determina el esfuerzo en un resorte con un módulo de Young equivalente a 300 Pa, si su deformación es de 30.

Un cuerpo de 1 kg de masa y dimensiones pequeñas está unido a un muelle de masa despreciable que tiene una longitud natural de 48 cm y una constante elástica de 980 N/m. Hacemos girar el muelle y el cuerpo que sostiene, como un péndulo cónico, a una frecuencia de 60 rpm, manteniendo fijo el extremo que no está unido al cuerpo.

a) Determina el alargamiento del muelle y el ángulo que forma el eje de rotación del sistema con la dirección del muelle, cuando está girando.

b) Tomando como origen (o cero) de energía potencial gravitatoria el plano horizontal que contiene el punto fijo del muelle, calcula la energía mecánica total del sistema.

Se hace girar una moneda de dos euros (2.575 cm de radio y 8.5 g de masa) alrededor de un eje contenido en el plano de la moneda y que pasa por su centro. Para ello se le aplica un par de fuerzas con los dedos durante 0.1 s y como resultado gira con una frecuencia de 10 rpm.

a) ¿Qué fuerza se aplicó a los bordes de la moneda?

b) ¿Qué fuerza habría que aplicar a una moneda de 1 euro (2.325 cm de radio y 7.5 g de masa) para que gire con la misma frecuencia que la de dos euros?

Considera que el momento de inercia de las monedas es: .

Imagina que sostienes un libro contra la pared apretándolo con la mano. La fuerza forma un ángulo con la pared, como se muestra en la figura:

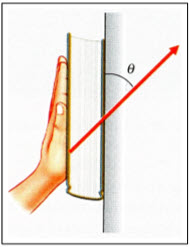
La masa del libro es m y el coeficiente de fricción estática es .

a) Calcula la magnitud de la fuerza que debes ejercer para (apenas) mantener el libro estacionario.

b) ¿Para qué valor del ángulo la magnitud de la fuerza requerida es la más pequeña posible? ¿Cuál es la magnitud de la menor fuerza posible?

c) Si empujas con un ángulo mayor de , debes hacerlo muy fuerte para sostener el libro en su lugar. ¿Para qué valor del ángulo se hará imposible sostener en su lugar al libro?