Un proyectil de 2.00 kg de masa se mueve a la derecha con una rapidez de . El proyectil golpea y se queda pegado a una distancia de d=3.00 m del extremo de una varilla de M = 5.00 kg y 4.00 m de longitud que cuelga verticalmente en reposo y hace pivote alrededor de un eje sin fricción que pasa por su extremo superior. Determina:

a) La rapidez angular del sistema inmediatamente después de la colisión.

b) La energía cinética del sistema antes de la colisión.

c) La energía cinética del sistema después de la colisión.

d) La degradación de energía durante la colisión.

Un esquiador que viaja a 9.0 m/s llega al pie de una pendiente hacia arriba de y se desliza 12 m a lo largo de esta pendiente antes de llegar al reposo. ¿Cuál es el coeficiente de fricción promedio?

En la figura se muestra el resultado de un choque entre dos objetos de masas distintas.

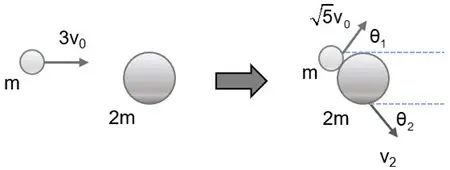
a) Calcula la velocidad de la masa mayor después del choque y el ángulo .

b) Demuestra que este choque es elástico.

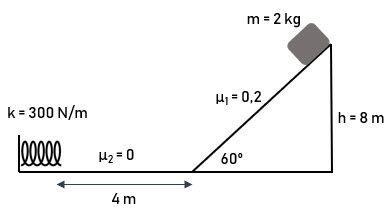
En la figura se muestra un bloque de 2 kg que se deja caer desde la parte alta de un plano inclinado con el que presenta un fricción con . Al final del recorrido se encuentra con un resorte con constante elástica . Calcula la máxima compresión que sufre el resorte.

Un resorte se comprime para lanzar verticalmente hacia arriba un objeto que alcanza una altura h. Para duplicar la altura alcanzada la compresión del resorte debe ser de:

a) .

b) .

c) .

d) Ninguna es correcta.

Una bala de 0.01 kg que se mueve horizontalmente golpea un bloque de madera de masa 1.5 kg suspendida de un hilo de 2 m de longitud. La bala se incrusta en la madera y éste sube una altura de 0.40 m. ¿Cuál era la velocidad de la bala en el instante anterior a golpear el bloque de madera?

En una práctica, una esfera de masa 1.98 kg que se desliza por una pista horizontal lisa (sin fricción) con una velocidad de 1.26 m/s y choca con un resorte de masa despreciable y constante k = 528 N/m en equilibrio y con uno de sus extremos fijo. A partir de la información anterior, calcula:

a) La distancia que se comprime el resorte.

b) La altura desde la que debería caer la esfera sobre el resorte, si este se coloca verticalmente, para producir la misma compresión del apartado anterior, asumiendo que en ese punto la esfera se detiene.

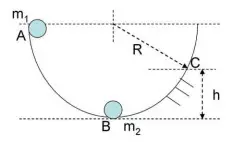
Un cuerpo de masa cae desde el punto A, partiendo del reposo, por una semiesfera de radio R = 3 m. En el punto B tenemos un segundo cuerpo de masa . Entre A y B no existe fricción. En el punto B se produce un choque de forma que ambos cuerpos quedan enganchados. Después ambos cuerpos se desplazan por el tramo BC con fricción hasta llegar a una altura h.

a) Calcula la energía degradada en el choque que se produce en B.

b) Calcula el valor de la fuerza normal aplicada sobre el nuevo cuerpo en el punto B, cuando tiene un movimiento circular, justo después del choque.

c) Calcula la altura máxima alcanzada en C si la energía degradada por fricción en el tramo BC vale una cuarta parte de la que tenía justamente después del choque.

Se lanza un cuerpo con una velocidad de desde la base de un plano inclinado en un ángulo . Se observa que el cuerpo alcanza una altura h = 6 cm sobre el nivel de la base del plano y luego, desde esa altura, vuelve a caer hasta la base del plano.

a) Razona si es un sistema conservativo o no.

b) ¿Cuánto es el coeficiente de rozamiento del plano?

c) ¿Con qué velocidad vuelve el cuerpo a la base del plano?

Un cuerpo de 1.5 kg se encuentra incicialmente comprimiendo 0.3 m un resorte de constante elástica de 800 N/m. Al liberar el resorte se desliza, sin rozamiento, por un riel y alcanza un tramo circular:

a) Sabiendo que la velocidad del cuerpo en el punto más alto del círculo es de 2.0 m/s, calcula el radio del tramo circular.

b) Al salir del tramo circular llega a un tramo rugoso de 3 m con coefciente de rozamiento de 0.25. ¿Cuál es la velocidad del cuerpo al atravesar ese tramo?