Ejercicios FyQ
Una esfera homogénea de masa M y radio R rueda sin deslizar desde el reposo hacia abajo en un plano inclinado, como se muestra en la figura.
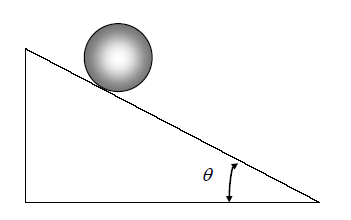
Halla:
a) La aceleración angular de la esfera.
b) El mínimo coeficiente de rozamiento para evitar el deslizamiento.
En una máquina de Atwood, dos bloques de masas 12 y 4 kg se desplazan con una aceleración desconocida conectados mediante una cuerda ideal a través de una polea sin fricción de masa 8 kg y radio 0.2 m. Calcula la aceleración de los bloques sabiendo que el momento de inercia de la polea es 
.
Una lámina uniforme de 5m de largo y 50 kilogramos de masa está sostenida horizontalmente por sus extremos mediante dos alambres verticales uno de acero (cuyo modulo de Young es 
) y otro de cobre (cuyo modulo de Young es de 
. Cada alambre tiene 3 metros de longitud y 
de sección transversal. Calcula el cambio de longitud de cada alambre.
Un francotirador quiere disparar a un blanco que se encuentra a 835 m de distancia y a una altura de 4.2 m sobre el punto desde el que dispara. Si el proyectil sale con una velocidad de 
, ¿con qué ángulo debe disparar para darle al blanco?
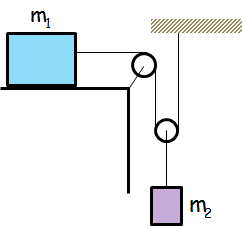
Determina la aceleración del bloque 2 en el siguiente sistema, suponiendo que no existen rozamientos:
En la figura puedes ver una versión simplificada de la molécula de agua.
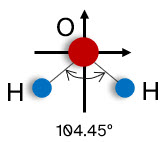
La longitud del enlace 
es 0.09584 nm y el ángulo de enlace 
es 
. El centro de masas de esta molécula, respecto a los ejes dibujados, está en el eje Y siendo el. ¿Cuál es el valor de su coordenada, expresada en nm?
Se sueldan, una a continuación de otra, dos varillas homogéneas A y B de la misma longitud «L», pero hechas de dos materiales diferentes, siendo la densidad de A doble que la de B. ¿A qué distancia del extremo de A se encuentra el centro de masas del sistema?
En los vértices de un cuadrado de lado a se sitúan cuatro masas tal como indica la figura.
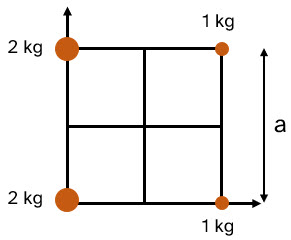
Si en medio de la recta que une las masas de 1 kg se sitúa una masa de M kilogramos resulta que el centro de masas del sistema formado está en el centro de dicho cuadrado. ¿Cuál debe ser el valor de la masa M?
Dos esferas de masas 
y 
están suspendidas de dos hilos paralelos de longitudes 
y 
respectivamente. En posición de equilibrio las esferas están con sus centros al mismo nivel. La masa se desvía lateralmente un ángulo 
y, a partir del reposo, se le deja en libertad. En su descenso choca con y, tras el impacto se desviará un ángulo máximo 
. Si el coeficiente de restitución es e, determina:
a) Las velocidades de las esferas después de chocar.
b) El ángulo que se desvía tras el choque.
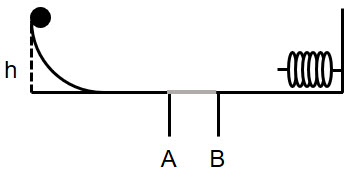
Un bloque de 10 kg en reposo se caer desde una altura h = 5 m sobre una rampa lisa y curva. Entre A y B, que distan 2 m, el rozamiento no es despreciable. Se sabe que la fuerza de fricción que se produce al pasar por este sector es de módulo 40 N. Tras este sector hay un resorte ideal de constante recuperadora k = 4 000 N/m contra el que choca el bloque, deformándolo:
a) Calcula la máxima elongación que sufre el resorte. ¿Qué sucede en ese instante de máxima compresión? ¿Qué sucede después de ese instante?
b) ¿A qué altura de la rampa llegará cuando ascienda por ella tras la primera deformación del resorte?
c) ¿Dónde se detiene el bloque? ¿Cuántas veces pasó por el sector con rozamiento antes de detenerse?
