-
Ampliación: energía mecánica de un coche que sube una montaña (6273)
Calcula la cantidad de energía mecánica total de un automóvil que se encuentra subiendo una montaña, sabiendo que tiene una masa de una tonelada, se encuentra a una altura de 500 m y lleva una rapidez de 50 km/h.
-
Estudio de un muelle que gira formando un péndulo cónico (6293)
Un cuerpo de 1 kg de masa y dimensiones pequeñas está unido a un muelle de masa despreciable que tiene una longitud natural de 48 cm y una constante elástica de 980 N/m. Hacemos girar el muelle y el cuerpo que sostiene, como un péndulo cónico, a una frecuencia de 60 rpm, manteniendo fijo el extremo que no está unido al cuerpo.
a) Determina el alargamiento del muelle y el ángulo que forma el eje de rotación del sistema con la dirección del muelle, cuando está girando.
b) Tomando como origen (o cero) de energía potencial gravitatoria el plano horizontal que contiene el punto fijo del muelle, calcula la energía mecánica total del sistema.
-
Conservación de la energía mecánica en sistema que degrada energía (6288)
Una pelota se arroja desde una altura de 110 metros con una velocidad inicial de 5 m/s. La masa de la pelota es de 3 kg. Calcula:
a) ¿Con qué velocidad golpea el objeto al suelo?
b) Si el objeto golpea el suelo y pierde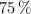 
de la energía, y rebota nuevamente hacia arriba, ¿cuál será la altura máxima que alcanzará la pelota con el rebote?
-
Velocidad de un esquiador y distancia que recorre antes de pararse (6186)
Un esquiador inicia su movimiento a partir del reposo, en la parte más alta de una pendiente, sin fricción, de 32 m de altura. Cuando llega a la parte más baja, encuentra una superficie horizontal donde el coeficiente de rozamiento cinético entre los esquís y la nieve es 0.18. Calcula, usando criterios energéticos:
a) La magnitud de la velocidad del esquiador cuando ha bajado 10 m (verticales) desde su punto de partida.
b) La distancia que recorre en la superficie horizontal antes de detenerse, si no se impulsa con los bastones.
-
Conservación de la energía en un sistema con tramos sin y con rozamiento (6096)
Un cuerpo de 1.5 kg se encuentra incicialmente comprimiendo 0.3 m un resorte de constante elástica de 800 N/m. Al liberar el resorte se desliza, sin rozamiento, por un riel y alcanza un tramo circular:
a) Sabiendo que la velocidad del cuerpo en el punto más alto del círculo es de 2.0 m/s, calcula el radio del tramo circular.
b) Al salir del tramo circular llega a un tramo rugoso de 3 m con coefciente de rozamiento de 0.25. ¿Cuál es la velocidad del cuerpo al atravesar ese tramo?
Energía mecánica
Ejercicios FyQ