-
Ecuación de la onda generada al agitar una cuerda (7537)
Se agita el extremo de una cuerda con una frecuencia de 2 Hz y una amplitud de 3 cm. Si la perturbación se propaga con una velocidad de 0.5 m/s, escribe la expresión que representa el movimiento por la cuerda.
-
Longitud de onda que produce el oscurecimiento de unas gafas de sol (6671)
Las lentes de ciertas gafas de sol tienen incorporados pequeños cristales de cloruro de plata (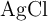
). Al exponerse a la luz de longitud de onda adecuada, sucede la siguiente reacción:
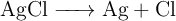
Los átomos de Ag formados producen un color gris uniforme que atenúa los reflejos. Si la entalpía de la reacción es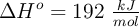 
, calcula la máxima longitud de onda de la luz que puede inducir este proceso.
-
Magnitudes características de una onda electromagnética plana sinusoidal (6664)
Una onda electromagnética plana sinusoidal se desplaza en el vacío en el sentido positivo del eje OX, siendo su frecuencia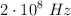 
y la amplitud máxima del campo eléctrico 
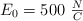, vibrando en el eje OY. Calcula:
a) La longitud de onda y el periodo.
b) La amplitud máxima del campo magnético y su dirección de vibración.
c) Las ecuaciones de los campos magnético y eléctrico de la onda.
-
Nodos y vientres de la onda estacionaria de un violonchelo (6421)
La longitud de la cuerda de un violonchelo es de 70 cm y la velocidad de propagación de las ondas en esta cuerda es de 308 m/s. Para el tercer armónico:
a) Representa esquemáticamente la onda estacionaria de este armónico indicando todos sus nodos y vientres. Calcula la longitud de onda. ¿Cuál es la distancia entre dos nodos consecutivos?
b) Suponiendo que la cuerda está en posición horizontal, calcula, para un vientre, el tiempo que tarda la posición vertical en pasar de su valor máximo a su valor mínimo (del punto más alto al punto más bajo).
-
Tamaño de los detalles que puede captar un ecógrafo (5994)
El emisor de ultrasonidos de un ecógrafo emite ondas de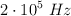 
que penetran en el cuerpo humano, donde su velocidad de propagación es de 
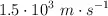. Si el aparato puede detectar detalles del tamaño de su longitud de onda, ¿cuál es el mínimo tamaño de los detalles que puede captar?
Longitud de onda
Ejercicios FyQ