-
Frecuencias de vibración de dos resortes con distinta longitud (6417)
De dos resortes con la misma constante elástica se cuelgan sendos cuerpos con la misma masa. Uno de los resortes tiene el doble de longitud que el otro, ¿los dos sistemas vibrarán con la misma frecuencia? Explica tu respuesta.
-
Relación de la elongación con la energía mecánica de un oscilador armónico (6371)
Una masa de 1 kg oscila unida a un resorte de constante k= 5 N/m, con movimiento armónico simple de amplitud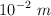 
.
a) Cuando la elongación es la mitad de la amplitud, calcula que fracción de la energía mecánica es cinética y que fracción es potencial.
b) ¿Cuánto vale la elongación en el punto en el que la mitad de la energía mecánica es cinética y la otra mitad potencial?
-
Análisis del movimiento armónico simple de una partícula sabiendo su frecuencia (6369)
Una partícula efectúa un MAS alrededor del punto x = 0. En t = 0, su posición es de x = 0 m y v = - 60 m/s. Si la frecuencia del movimiento es de 50 Hz, determina:
a) Frecuencia angular.
b) La rapidez máxima.
c) Aceleración máxima.
d) Posición en t = 6 s.
e) Velocidad en t = 12 s.
-
Aceleración de un MAS para un valor de amplitud dado
La posición, en cm, de un MAS viene dada por la ecuación: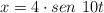 
, donde t es el tiempo en s. Calcula la aceleración en el instante en que la amplitud es 3 cm.
-
Estudio de la posición del péndulo de un reloj y su periodo
El péndulo de un reloj se mueve periódicamente, separándose s (cm) de la vertical. La ecuación que describe el movimiento es:
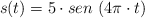
a) Decide a qué distancia de la vertical y de que lado de la misma estará el péndulo a los 2 s.
b) ¿Qué distancia máxima alcanza?
c) ¿En qué instante alcanza la distancia máxima?
d) ¿Cuál es su periodo?
Movimiento armónico simple
Ejercicios FyQ