Función onda

(19) ejercicios de Función onda

(#7545) Seleccionar

Ecuación de una onda armónica transversal a partir de varios datos (7545)

Una onda armónica transversal se propaga en el sentido positivo del eje OX a 90 km/h, tiene una amplitud de 2 m y una frecuencia de 80 Hz. En el instante inicial, en un punto situado en x = 1.25 m, tiene una elongación máxima positiva. Determina lo siguiente: frecuencia angular, longitud de onda, número de onda, periodo, ecuación de onda para cuando t = 0.01 s.
(#6664) Seleccionar

Magnitudes características de una onda electromagnética plana sinusoidal (6664)

Una onda electromagnética plana sinusoidal se desplaza en el vacío en el sentido positivo del eje OX, siendo su frecuencia 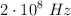$2\cdot 10^8\ Hz$ y la amplitud máxima del campo eléctrico 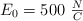$E_0 = 500\ \textstyle{N\over C}$ , vibrando en el eje OY. Calcula:

a) La longitud de onda y el periodo.

b) La amplitud máxima del campo magnético y su dirección de vibración.

c) Las ecuaciones de los campos magnético y eléctrico de la onda.
(#6418) Seleccionar

Ecuación de onda de la ola que hace el público de un estadio (6418)

En un estadio el público se hace la ola para celebrar la buena actuación del equipo local. La ola es tan grande que dos espectadores de la misma fila separados por un mínimo de 50 m se mueven igual y lo hacen cada 10 s.

a) Si se ’’modelizase’’ esta ola en el estadio como una onda, ¿de qué tipo de onda se trataría? Calcula su longitud de onda y la pulsación (frecuencia angular).

b) Un espectador se mueve 1.0 m verticalmente cuando se levanta y se sienta al hacer la ola. Escribe la ecuación del movimiento de este espectador considerando que describe un movimiento armónico simple y que en el instante inicial está sentado, es decir, en su posición mínima.

c) Escribe la ecuación de ondas de la ola.
(#5830) Seleccionar

Ecuación de una onda a partir de A, f y v (5830)

Si la onda en una cuerda tensa tiene una amplitud de 0.5 m , una frecuencia de 20 Hz y una velocidad de propagación de 10 m/s, escribe la ecuación de la onda.
(#5829) Seleccionar

Ecuación de una onda cuando cambia su velocidad pero no su frecuencia (5829)

Una onda que tiene una ecuacion, en unidades SI:

$y = 0.4\cdot cos \left[\pi \left(\frac{x}{2} - \frac{t}{4}\right) \right]$

Pasa del medio en el que se propagan a otro donde su velocidad se duplica y su amplitud se reduce a la mitad. Escribe la ecuación de propagación de la onda en el segundo medio, considerando que la frecuencia permanece constante.