-
Trabajo desarrollado por cada una de las fuerzas de un sistema (7312)
Un bloque de 75 kg es arrastrado desde el punto A hasta el punto B del plano inclinado por una fuerza F con una aceleración de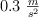 
. Si la superficie es rugosa y tiene un coeficiente de rozamiento de 0.68, calcula:
a) El trabajo realizado por la fuerza F.
b) El trabajo realizado por la normal.
c) El trabajo realizado por el peso.
d) El trabajo realizado por la fuerza de rozamiento.
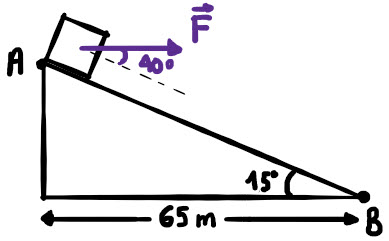
Fuerza rozamiento
-
Peso máximo de un bloque para que el sistema permanezca en equilibrio (7311)
El bloque B en la pesa 711 N. El coeficiente de fricción estática entre el bloque B y la mesa es 0.25 y el ángulo es de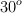 
. Suponiendo que la cuerda entre B y el nudo es horizontal, ¿cuál es el peso máximo del bloque A para el que el sistema estará en equilibrio?
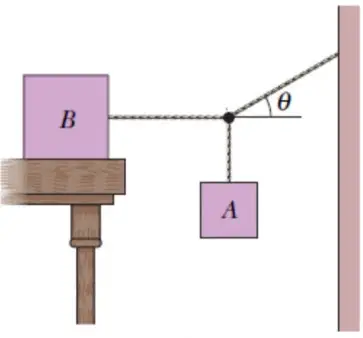
Fuerza rozamiento
-
Fuerza de fricción necesaria para que un sistema esté equilibrio (7309)
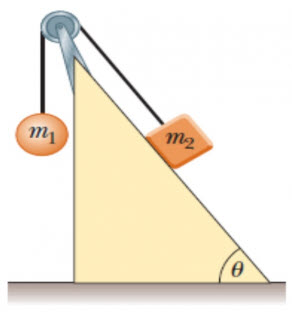
Dos objetos están conectados por una cuerda que pasa por una polea sin fricción como se muestra en la figura. Suponiendo que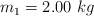 
, 
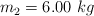y un ángulo de 
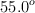, determina la fuerza de fricción necesaria para que el sistema se mantenga en equilibrio.
Fuerza rozamiento
-
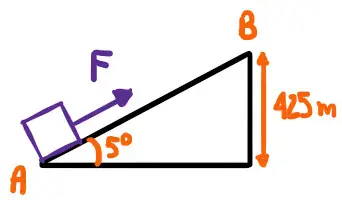
Potencia y fuerza de una locomotora que asciende una pendiente (7305)
Una locomotora de 350 toneladas es acelerada mientras asciende por una pendiente desde el punto A hasta el punto B, aumentando su velocidad desde los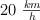 
hasta los 
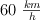, como se puede ver en la figura:
Fuerza rozamiento
Si el coeficiente de rozamiento es 0.15, determina:
a) La potencia desarrollada por la fuerza de rozamiento.
b) La potencia desarrollada por el peso.
c) La fuerza desarrollada por la locomotora.
d) La potencia desarrollada por la fuerza anterior.
-
Fuerza de rozamiento y normal sobre una podadora empujada por una persona (7290)
Una persona empuja una podadora de 14 kg con una rapidez constante y una fuerza de F = 100 N dirigida a lo largo del manubrio, que forma un ángulo de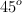 
con la horizontal.
Fuerza rozamiento
a) Calcula la fuerza de fricción horizontal sobre la podadora.
b) La fuerza normal ejercida verticalmente hacia arriba sobre la podadora por el suelo.
c) ¿Qué fuerza debe ejercer la persona sobre la podadora para acelerar desde el reposo hasta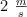 
en 4 s, suponiendo la misma fuerza de fricción?
Fuerza rozamiento
Ejercicios FyQ