-
Constante elástica de un resorte y trabajo realizado sobre él (5895)
Durante un entrenamiento un deportista, que tiene una masa corporal de 63.0 kg, se sube a una báscula de funcionamiento mecánico que utiliza un resorte rígido. En equilibrio, el resorte se comprime 1.25 cm bajo su peso. Con base en la anterior información determina:
a) La constante de elasticidad del resorte.
b) El trabajo total efectuado sobre él durante la compresión.
-
Ampliación: aplicación de la ley de Hooke (5865)
Se dispone de dos cuerpos y de un resorte elástico (muelle). Si se conoce la masa de uno de los cuerpos, ¿cómo podríamos averiguar la masa desconocida del otro cuerpo?
-
Ampliación: Constante recuperadora y longitud inicial de un resorte (5792)
Un resorte de constante desconocida es puesto en un tubo cilíndrico de forma tal que se pueda medir la deformación ante la presencia de distintos objetos encima de este. Dicho resorte se deforma un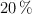 
de su longitud normal con una masa de 5 kg. Si colocamos una masa de 2 kg se deforma 5 cm. ¿Cuál es el valor de la constante recuperadora del resorte y su longitud inicial?
-
Deformación de un resorte cuando se cuelga el triple de masa (5681)
Un cuerpo de 600 g se suspende de un resorte vertical y este se deforma 0.2 m. Determina qué deformación se producirá en el resorte si se usa un cuerpo cuya masa es el triple que la del primero.
-
Dos esferas unidas por un resorte se cargan eléctricamente y alcanzan un equilibrio (5590)
Dos esferas idénticas inicialmente descargadas se unen con un resorte no conductor de longitud inicial 1 m, cuya constante elástica es de 25 N/m. Un instante después las esferas son cargadas con cargas iguales y de signo contrario +q y -q y el resorte se contrae hasta alcanzar una longitud de 0.635 m. Encuentra el valor de la carga q que genera la situación de equilibrio. Discute sobre lo que hubiese ocurrido si el resorte estuviese recubierto de un material metálico.
Ley de Hooke
Ejercicios FyQ