-
Posición, velocidad y momentos angular y lineal de un sistema de dos partículas (6158)
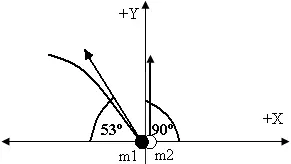
La figura muestra un sistema formado por dos partículas con masas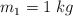 
y 
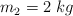. Las partículas se lanzan simultáneamente y sus velocidades iniciales son 
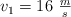y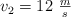 
. Para el instante t = 2 s, determina:
a) La posición del centro de masas del sistema respecto al origen.
b) La velocidad del centro de masas del sistema respecto al origen.
c) El momento angular del sistema respecto al origen.
d) El momento lineal de la partícula 1 respecto al centro de la masas.
Velocidad
-
Aceleración, velocidad y distancia que recorre un grupo y un ciclista escapado (6122)
En una carrera, un grupo de ciclistas parten del reposo. A cabo de 8.5 s uno de ellos ha alcanzado una velocidad de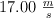 
, mientras que el resto alcanzó los 
.
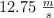a) Determina las aceleraciones medias en cada caso.
b) Suponiendo que el cambio en el valor de la velocidad fue constante, elabora los gráficos de velocidad en función del tiempo.
c) ¿Cuál fue el desplazamiento en esos 8.5 s en ambos casos?
-
Aceleración, posición y velocidad de un cuerpo con movimiento uniformemente acelerado (6095)
Un cuerpo que se encontraba inicialmente reposo comienza a moverse en línea recta y con aceleración constante y al cabo de 5 s adquiere una velocidad de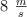 
. A partir de esta situación, calcula:
a) La aceleración del cuerpo.
b) La posición del cuerpo al cabo de 5 s.
c) La velocidad del cuerpo después de 8 s.
-
Velocidad, rapidez y posición de una partícula a partir de su aceleración (6025)
En t = 0, una partícula parte del reposo en x = 5 m e y = 8 m, y se mueve en el plano XY con una aceleración de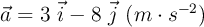 
. Determina:
a) Las componentes X e Y de la velocidad en t = 4 s.
b) La rapidez de la partícula en t = 4 s.
c) La posición de la partícula en t = 8 s.
-
Distancia entre dos destinos y velocidad para llegar a tiempo (5936)
El conductor de un tren sale de su destino a una velocidad de 100 km/h y se da cuenta que llegará con una hora de retraso a su destino, por lo que decide acelerar a una velocidad de 150 km/h, aunque se da cuenta de que a esa velocidad llegará con una hora de anticipación.
a) ¿A qué velocidad debe marchar para llegar puntualmente a su destino?
b) ¿Cuál es la distancia entre el punto de salida y punto de llegada?
Velocidad
Ejercicios FyQ