-
Nombrar compuestos orgánicos con un carbono quiral (8439)
Nombra los siguientes compuestos:
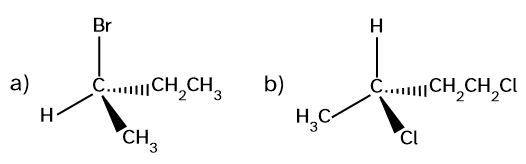
RESUELTO
-
Análisis de la quiralidad de varios compuestos orgánicos (8437)
¿Cuáles de los siguientes compuestos tiene un centro asimétrico?
a) ![\chemfig{CH_3-CH_2-CH(-[2]Cl)-CH_3} \chemfig{CH_3-CH_2-CH(-[2]Cl)-CH_3}](local/cache-TeX/5b31db9ea22f557346702791424f673a.png)
b) ![\chemfig{CH_3-CH_2-CH(-[2]CH_3)-CH_3} \chemfig{CH_3-CH_2-CH(-[2]CH_3)-CH_3}](local/cache-TeX/d22b412246c479ba9b766db7ae6d0446.png)
c) ![\chemfig{CH_3-CH_2-C(-[2]CH_3)(-[6]Br)-CH_2-CH_2-CH_3} \chemfig{CH_3-CH_2-C(-[2]CH_3)(-[6]Br)-CH_2-CH_2-CH_3}](local/cache-TeX/c3643f130471d9dde151b8ca95c16a3c.png)
d) 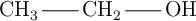
e) ![\chemfig{CH_3-CH_2-CH(-[2]Br)-CH_2-CH_3} \chemfig{CH_3-CH_2-CH(-[2]Br)-CH_2-CH_3}](local/cache-TeX/2075e71c72fbc0e51821d17ae7d9e4ad.png)
f) ![\chemfig{CH_2=CH-CH(-[2]NH_2)-CH_3} \chemfig{CH_2=CH-CH(-[2]NH_2)-CH_3}](local/cache-TeX/4b802e6570fec64b20ec6db3c69eaa24.png)
-
Ampliación: tensión de una cuerda para que un sistema esté en equilibrio (8443)
Determina la tensión en la cuerda marcada, si p = 100 N.
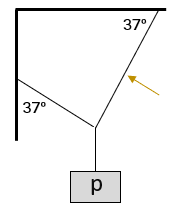
RESUELTO
-
Contracción de la longitud y dilatación del tiempo en una nave espacial a gran velocidad (8436)
Un astronauta viaja en una nave espacial a una velocidad de 0.8c (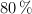 de la velocidad de la luz) con respecto a la Tierra. La nave espacial tiene una longitud propia (medida por el astronauta en su propio marco de referencia) de 100 metros.
de la velocidad de la luz) con respecto a la Tierra. La nave espacial tiene una longitud propia (medida por el astronauta en su propio marco de referencia) de 100 metros.
a) ¿Qué longitud tiene la nave espacial según un observador en la Tierra?
b) Si el astronauta mide un pulso de luz que tarda 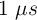 en recorrer la longitud de la nave, ¿cuánto tiempo mide un observador en la Tierra que el pulso de luz tarda en recorrer la misma distancia?
en recorrer la longitud de la nave, ¿cuánto tiempo mide un observador en la Tierra que el pulso de luz tarda en recorrer la misma distancia?
c) Un observador en la Tierra ve pasar la nave espacial. ¿Cuánto tiempo tarda, según este observador, en pasar completamente la nave por un punto dado?
-
Notación de Fischer y estereoisómeros de un compuesto con dos carbonos quirales (8438)
Considera la siguiente molécula orgánica:
![\chemfig{CH_3-CH(-[6]OH)-CH(-[6]CH_3)-CH_2OH} \chemfig{CH_3-CH(-[6]OH)-CH(-[6]CH_3)-CH_2OH}](local/cache-TeX/3c34ee12cba07d1b3cf054f77d96b999.png)
a) Identifica los centros quirales en esta molécula.
b) Dibuja todos los posibles estereoisómeros de este compuesto utilizando la notación de cuña y guion (o la notación de Fischer si lo prefieres).
c) Indica la relación entre los estereoisómeros que has dibujado (enantiómeros, diastereoisómeros, meso).
 RESUELTO
RESUELTO