-
Velocidad de una oscilación producida por el estiramiento de un resorte (7070)
Un resorte está sobre una superficie horizontal y tiene atada una masa de 800 g. Se le aplica una fuerza de 100 N hasta deformarlo 16 cm desde su punto de equilibrio. Se suelta de tal forma que se produce un MAS, calcula:
a) ¿Cuál es la constante k del resorte?
b) ¿Cuál es su velocidad máxima?
c) ¿Cuál es la velocidad en x = 10 cm?
-
Periodo para pequeñas oscilaciones de una masa en un campo unidimensional (6803)
Una partícula de masa «m» se encuentra en un campo potencial unidimensional, donde su energía depende de la coordenada «x» según la ley ![U = U_0 [1 - cos\ (ax)]](local/cache-TeX/78ba7776c6837cd2caf4f8d32ab3d749.png "U = U_0 [1 - cos\ (ax)]")
, en donde «a» y «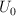
» son constantes. Determina el periodo para pequeñas oscilaciones.
-
Frecuencia, y ecuación del movimiento de un muelle que oscila (6564)
Al colocar un bloque de 2 kg suspendido de un muelle se produce un alargamiento de 4 cm. Si a continuación se le estira 5 cm y se suelta dejándolo oscilar libremente, el bloque describe un MAS. Calcula:
a) La constante recuperadora del muelle.
b) La frecuencia de las oscilaciones.
c) La ecuación del movimiento.
-
Parámetros de la oscilación de un objeto que cuelga de un resorte (5946)
Un objeto se encuentra en la parte inferior de un resorte en reposo. El peso del objeto es de 1 lbf y la elongación del resorte es 8 cm. Halla:
a) La constante elástica del resorte.
b) La masa del objeto.
c) La amplitud.
d) La velocidad angular.
e) La velocidad lineal.
f) La aceleración.
g) El periodo.
-
Movimiento armónico simple: Masa unida a un resorte (1535)
Un cuerpo de 5 kg está unido a un resorte y oscila con una amplitud de 6 cm y una frecuencia de 4 Hz:
a) ¿Cuál es la constante recuperadora del resorte?
b) ¿Cuál es el periodo del movimiento?
c) ¿Cuáles son la velocidad y aceleración máximas?
Constante recuperadora
Ejercicios FyQ