-
Ecuación que permite calcular la fuerza necesaria para que una escalera esté en equilibrio sobre la pared (7574)
Una escalera de peso W y longitud L se apoya sobre una pared sin rozamiento. Sobre la escalera se encuentra una persona de peso P, a una distancia S del pie de la escalera, medida a lo largo de esta. El pie de la escalera se encuentra a una distancia D de la esquina inferior de la pared. Determina una expresión para la fuerza que la pared ejerce sobre la escalera, considerando que el sistema se encuentra en equilibrio estático.
-
Peso máximo de un bloque para que el sistema permanezca en equilibrio (7311)
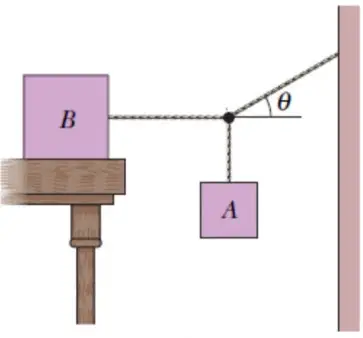
El bloque B en la pesa 711 N. El coeficiente de fricción estática entre el bloque B y la mesa es 0.25 y el ángulo es de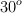 
. Suponiendo que la cuerda entre B y el nudo es horizontal, ¿cuál es el peso máximo del bloque A para el que el sistema estará en equilibrio?
Estática
-
Fuerza para sujetar un libro contra la pared (7164)
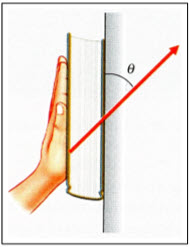
Imagina que sostienes un libro contra la pared apretándolo con la mano. La fuerza forma un ángulo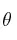 
con la pared, como se muestra en la figura:
Estática
La masa del libro es m y el coeficiente de fricción estática es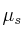 
.
a) Calcula la magnitud de la fuerza que debes ejercer para (apenas) mantener el libro estacionario.
b) ¿Para qué valor del ángulo 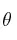la magnitud de la fuerza requerida es la más pequeña posible? ¿Cuál es la magnitud de la menor fuerza posible?
c) Si empujas con un ángulo mayor de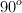 
, debes hacerlo muy fuerte para sostener el libro en su lugar. ¿Para qué valor del ángulo se hará imposible sostener en su lugar al libro?
-
Tensiones de las cuerdas de un sistema en equilibrio (6778)
Halla el valor de las tensiones del esquema:
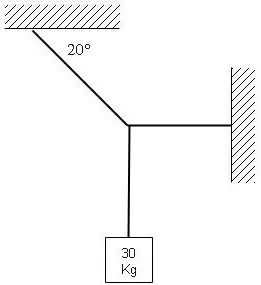
Estática
-
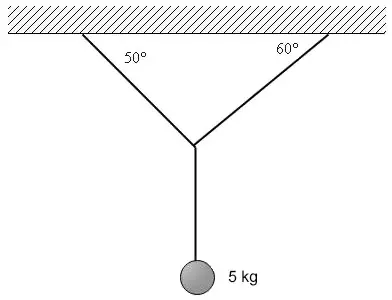
Tensiones en las cuerdas que sujetan una masa (6774)
Halla las tensiones de las cuerdas del sistema:
Estática
Estática
Ejercicios FyQ