Energía potencial gravitatoria

(145) ejercicios de Energía potencial gravitatoria

(#5631) Seleccionar

Altura máxima de un móvil lanzado con una energía de mil julios (5631)

Halla la altura máxima que alcanza un móvil de 4 kg que es lanzado verticalmente hacia arriba con una energía de mil julios.
(#5628) Seleccionar

Deformación que sufre un resorte cuando le cae un cuerpo desde 1 m de altura (5628)

Un cuerpo de 0.5 kg se deja caer libremente desde 1 m de altura sobre un pequeño resorte que está sujeto al suelo y en posición vertical, cuya constante elástica es 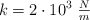$k = 2\cdot 10^3\ \textstyle{N\over m}$ . ¿Cuál será la deformación máxima que experimenta el resorte?
(#5591) Seleccionar

Estudio de energía mecánica y velocidad en distintos sistemas

Con los datos de la siguiente foto, calcula:

1. La velocidad con la que llegaría al suelo una pelota que cae desde lo alto de la torre Eiffel.

2. Si cae una pelota desde lo alto del barco puesto en vertical, ¿qué velocidad llevaría al pasar a la misma altura que tiene el punto más alto de la Sagrada Familia?

3. ¿Con qué velocidad tendríamos que lanzar un objeto desde el suelo para que llegue a lo alto del Big Ben?

4. Si lanzo verticalmente y hacia abajo un objeto desde la Torre de Pisa con una velocidad de 4 m/s, ¿con qué velocidad llegará al suelo?

5. Si a un pasajero que está en la cubierta superior se le caen las gafas, ¿con qué velocidad verá pasar las gafas otro pasajero que está en su camarote a la mitad de la altura máxima del barco?

Energía potencial gravitatoria
(#5584) Seleccionar

Trabajo de rozamiento en una superficie curva

Un paquete de 0,2 kg se suelta desde el reposo desde lo alto de una vía que forma un cuarto de círculo de radio 1,6 m. El paquete se desliza por la vía y llega al punto más bajo con una velocidad de 4,8 m/s. ¿Cuál es el trabajo que realiza la fricción durante el recorrido?
(#5583) Seleccionar

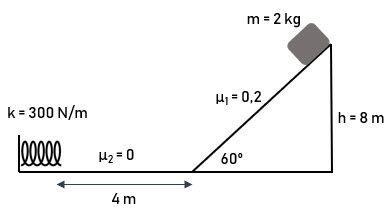
Comprensión de un resorte al golpear un bloque que cae por un plano inclinado (5583)

En la figura se muestra un bloque de 2 kg que se deja caer desde la parte alta de un plano inclinado con el que presenta un fricción con 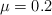$\mu = 0.2$ . Al final del recorrido se encuentra con un resorte con constante elástica 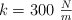$k = 300\ \textstyle{N\over m}$ . Calcula la máxima compresión que sufre el resorte.

Energía potencial gravitatoria