Módulo

(7) ejercicios de Módulo

(#8323) Seleccionar

Representación y cálculo de vectores de desplazamiento (8323)

a) Representa gráficamente los puntos A(0,4), B(-2,0) y C(5,3) y dibuja los vectores posición, con respecto al origen, 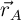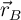$\vec{r}_A$ , $\vec{r}_B$ y $\vec{r}_C$ .

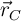b) Escribe analíticamente los vectores representados en el apartado anterior.

c) Calcula los vectores que describen el desplazamiento de A a B (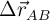 $\Delta \vec{r}_{AB}$ ) y de A a C ( 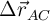$\Delta \vec{r}_{AC}$ ), y represéntalos gráficamente.

d) Calcula el módulo de ambos desplazamientos e interpreta el resultado obtenido.
(#7207) Seleccionar

Vector unitario en la dirección de un vector resultante (7207)

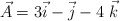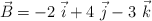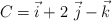Se dan los siguientes vectores $\vec A = 3\vec i - \vec j - 4\ \vec k$ , $\vec B = -2\ \vec i + 4\ \vec j - 3\ \vec k$ y $C = \vec i + 2\ \vec j - \vec k$ . Halla un vector unitario en la dirección del vector $3\vec A - 2\vec B +4\vec C$ .
(#7188) Seleccionar

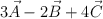Componentes, módulos y producto vectorial de vectores (7188)

A partir de la figura siguiente:

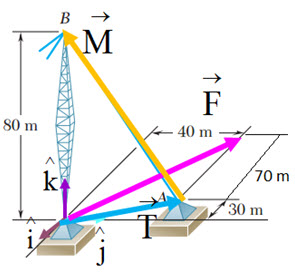
Módulo

a) Expresa los vectores en función de sus componentes.

b) Calcula el módulo de cada vector.

c) Calcula el producto vectorial 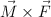$\vec M \times \vec F$ .
(#6332) Seleccionar

Valor de una fuerza perpendicular a partir del valor de la otra fuerza y la resultante (6332)

El módulo de la resultante de dos fuerzas perpendiculares que actúan sobre el mismo cuerpo es de 25 N. Si el módulo de una de ellas es de 24 N, ¿cuál es el de la otra?
(#5903) Seleccionar

Vector y módulo de la fuerza resultante sobre cuerpo que varía su velocidad (5903)

Un cuerpo de masa 1.5 kg tiene una velocidad inicial 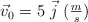$\vec v_0 = 5\ \vec j\ (\textstyle{m\over s})$ . El cuerpo es acelerado constantemente durante 5 s, siendo su velocidad 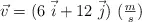$\vec v = (6\ \vec i + 12\ \vec j)\ (\textstyle{m\over s})$ . ¿Cuál es la fuerza neta sobre el cuerpo y su módulo durante los 5 s?