Los vectores y tiene módulos de 30 y 45 unidades respectivamente. Sus vectores unitarios son:

y

Sabiendo que , calcula el vector resultante de la operación:

¿Cuál es el vector unitario de ?

Determina las componentes rectangulares de una velocidad () que forma un angulo de con el eje positivo de abscisas.

Halla las componentes de un vector de 10 unidades de módulo y cuya dirección forma un angulo de con la horizontal.

Una espeleóloga está explorando una cueva. Sigue un pasadizo de 315 metros, al este del norte, luego otro de 533 metros, al oeste del sur y después de otro de 133 metros, al oeste del norte. Tras un cuarto desplazamiento no medido, vuelve al punto inicial. Determina el vector, desplazamiento y dirección del cuarto desplazamiento.

Mientras explora una cueva, una espeleóloga empieza a caminar en la entrada y avanza las siguientes distancias: 75 m al norte, 250 m al este, 125 m en un ángulo de al noreste y 150 m al sur. Encuentra el desplazamiento resultante desde la entrada de la cueva.

Calcula el vector necesario para que la resultante sea nula, si ya tengo dos vectores que son: y .

a) Representa gráficamente los puntos A(0,4), B(-2,0) y C(5,3) y dibuja los vectores posición, con respecto al origen, , y .

b) Escribe analíticamente los vectores representados en el apartado anterior.

c) Calcula los vectores que describen el desplazamiento de A a B () y de A a C (), y represéntalos gráficamente.

d) Calcula el módulo de ambos desplazamientos e interpreta el resultado obtenido.

Para los siguientes vectores: , y . Calcula .

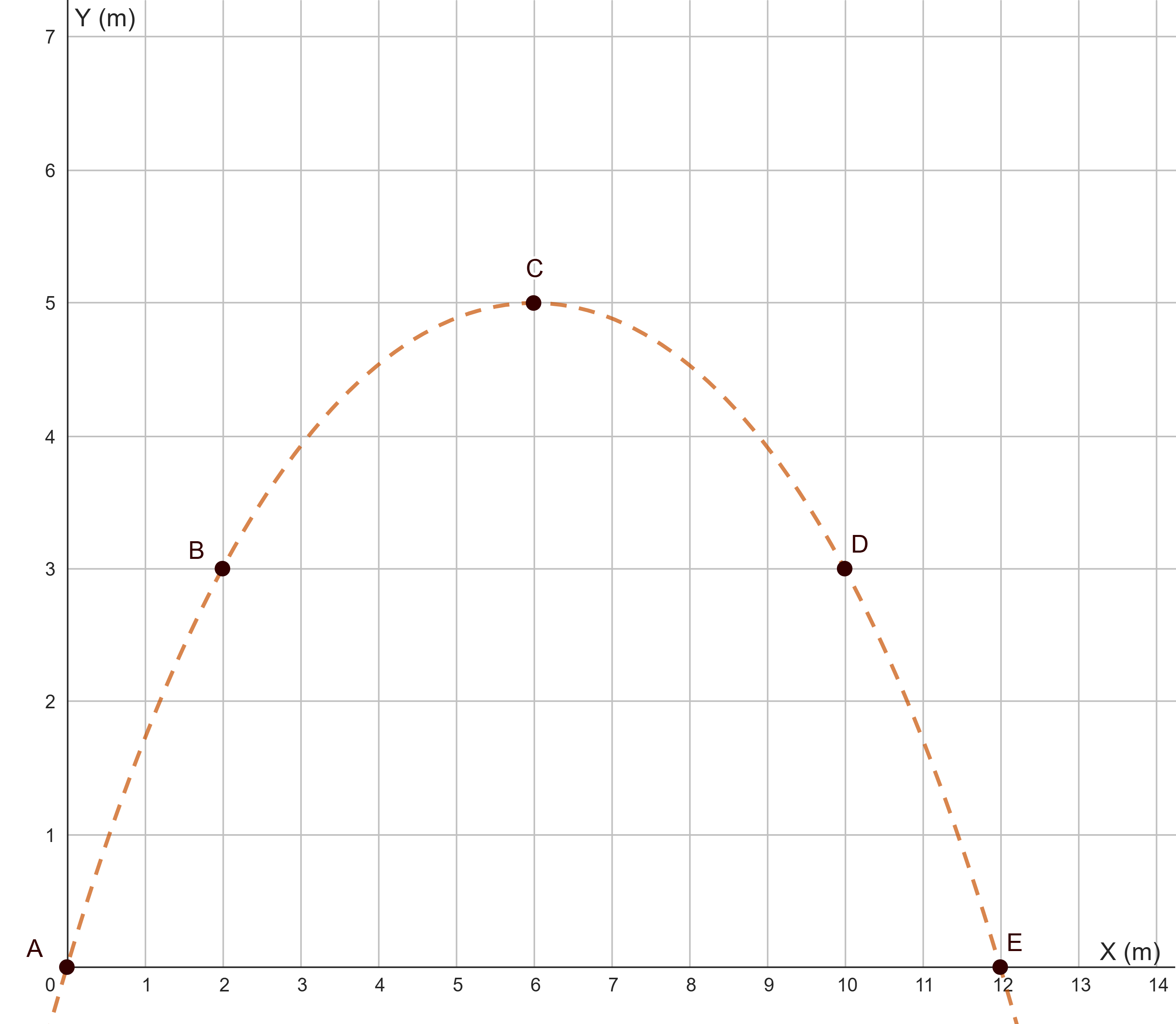
A partir del gráfico siguiente, dibuja los vectores de posición de cada uno de los puntos marcados y el desplazamiento entre los puntos B y D.