Ejercicios Resueltos de Vectores, Cinemática, Dinámica y Energía (2.º Bach)

Demuestra que la desigualdad , se cumple para los vectores y . ¿Qué tienen que cumplir dos vectores y para que se verifique la igualdad

En una competición, un deportista empuja durante 5 segundos a su compañera de 36 kg que está sentada sobre un deslizador por un camino para que gane impulso partiendo del reposo. El recorrido consta de 100 metros de un camino inclinado, que tiene con respecto a la horizontal, de hormigón donde la fricción se puede considerar nulo. Luego el camino es horizontal y el coeficiente de fricción dinámico entre las ruedas y el asfalto es de 0,1 hasta que se detiene. La fuerza que le aplica el deportista a la compañera es de 15 N en sentido descendente.

a) Calcula la longitud total del recorrido y el tiempo del recorrido.

b) Calcula la energía mecánica en el punto inicial, tras el empuje del deportista, al final del camino inclinado y al final del recorrido.

La distancia del puesto del lanzador de beisbol a la base es de 18.4 m. El terraplén donde se sitúa el lanzador está 0.2 m sobre el nivel del campo. Al lanzar una pelota con una velocidad inicial de 37.5 m/s, la mano del lanzador está a una altura de 2.3 m sobre el terraplén.

a) ¿Qué ángulo debe formar la velocidad inicial y la horizontal para que la pelota cruce la base a una altura de 0.7 m por encima del suelo?

b) ¿Con qué velocidad llega la pelota a la base?

Una persona lanza directamente hacia arriba una pelota de béisbol. La pelota tarda 3,5 s en alcanzar su altura máxima. Considera las magnitudes conocidas y explica un procedimiento para determinar dicha altura.

En un ascensor, que se mueve hacia arriba con rapidez constante de 6 m/s, una persona deja caer una moneda de su mano con una altura de 1.2 m con respecto al suelo del ascensor. ¿Cuánto tiempo tarda la moneda en llegar al suelo del ascensor?

Un bloque de 500 g se encuentra en reposo sobre una superficie horizontal sin rozamiento y unido a un resorte de constante elástica k = 300 N/m, cuando una bala de 5 g lo impacta con una velocidad de 1 000 m/s. Calcula:

a) ¿Cuál será la velocidad del bloque inmediatamente después del impacto?

b) ¿Cuál será la compresión máxima del resorte?

Un automotor parte del reposo y se mueve en una vía circular de 400 m de radio con un movimiento uniformemente acelerado. A los 50 s de iniciada la marcha alcanza la velocidad de 72 km/h, desde ese momento conserva esa velocidad. Calcula:

a) La aceleración en la primera fase del movimiento.

b) La aceleración normal, la aceleración total y la longitud de vía recorrida al final de los 50 s.

c) Velocidad angular media en la primera etapa.

d) La velocidad angular al final de los 50 s.

e) El tiempo que tardará en dar 100 vueltas al circuito.

Dos automóviles A y B viajan en línea recta. La posición de A respecto al punto de partida está dada por la ecuación (en unidades SI), y para el automóvil B la posición está dada por (también en unidades SI).
a) ¿Qué automóvil lleva la delantera justo un segundo después de salir del punto de partida?
b) ¿En qué tiempo los automóviles están en la misma posición?
c) ¿En qué tiempo tienen la misma velocidad?

A partir de la figura siguiente:

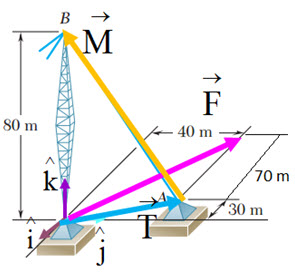
a) Expresa los vectores en función de sus componentes.

b) Calcula el módulo de cada vector.

c) Calcula el producto vectorial .

Una esfera de masa M pende sostenida por una barra rígida de masa despreciable y largo L. Una bala de masa m se dispara horizontalmente contra la esfera y la atraviesa. Al salir, la bala tiene la mitad de la rapidez que tenía antes de entrar y continúa su trayectoria recta. Llamando a la rapidez de la bala al impactar, encuentra:

a) La rapidez de la masa M, inmediatamente después del choque.

b) La rapidez mínima con que debe impactar la bala a la esfera para que esta realice una trayectoria circular completa tras ser atravesada por la bala.