En una mesa hay un taco de madera de 500 g unido, mediante un hilo que pasa por una polea de masa despreciable, a una pesa de 250 g que cuelga. Si el coeficiente de rozamiento entre el taco y la mesa es 0.25, calcula:

a) La aceleración del sistema.

b) La tensión de la cuerda.

En el sistema de la figura:

La fricción en la superficie es de 0,25 y la masa de la polea es despreciable. Si , y F = 1,5 N, encuentra:
a) La aceleración del sistema.
b) La tensión en las cuerdas.

Un bloque de masa está sobre una superficie horizontal lisa y unido, mediante una cuerda delgada que pasa sobre una polea, a un segundo bloque de masa , que cuelga libre verticalmente. Aplica la segunda ley de Newton para encontrar las fórmulas para la aceleración del sistema y para la tensión de la cuerda y calcula el valor de cada una de ellas. Ignora la fricción y las masas de la polea y la cuerda.

Un bloque se encuentra en un plano inclinado sin fricción como el de la figura. Si la masa del bloque es de 7 kg y el ángulo del plano es :

a) ¿Cuál es la aceleración?

b) ¿Cuál es valor de la fuerza normal?

c) ¿Qué distancia recorre, suponiendo que parte del reposo, en 5 s?

d) Resuelve el apartado anterior suponiendo que el coeficiente de rozamiento cinético de 0.18.

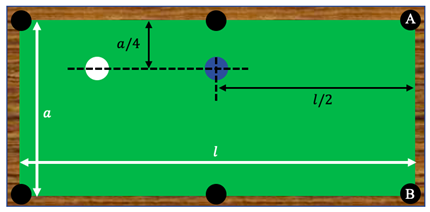
En un juego de billar, un jugador se dispone a realizar el tiro final para ganar el juego sobre una mesa de billar de dimensiones (l = 2.81 m) y (a = 1.65 m). Para que el tiro sea válido, la bola azul debe insertarse en el hueco A y la bola blanca no debe finalizar en el hueco B. Si el jugador dispara horizontalmente la bola blanca con una rapidez de 1.23 m/s y la bola azul sale directa hacia el hueco A con la mitad de la rapidez de la rapidez inicial de la bola blanca, ¿ganará el jugador la partida?

Tres partículas de masas 3m, 2m y m, con celeridades 3v, 2v y v, respectivamente, confluyen en un punto como se muestra la figura. La partícula 1 se mueve con una velocidad paralela al eje X, mientras que las partículas 2 y 3 se mueven con velocidades en las direcciones determinadas por los ángulos y , como se muestra en la figura. Después de la colisión las tres partículas permanecen unidas.

a) Determina analíticamente, y en función de las variables suministradas en el enunciado, el momento total antes del choque, expresado vectorialmente en términos de los vectores unitarios y .

b) La velocidad final, expresada vectorialmente en términos de los vectores unitarios y , de las partículas unidas después del choque.

Para el conjunto de valores m = 5.70 kg, v = 7.30 m/s, y , determina numéricamente:

c) Los resultados obtenidos los apartados a) y b).

d) La dirección de la velocidad final de las masas unidas.

Una caja con frutas y verduras de 15 kg de masa es liberada desde el reposo en la parte superior de una rampa sin fricción de 3 m de longitud, con una inclinación respecto a la horizontal. Se desliza hacia abajo alcanzando una velocidad de cuando llega a la base del plano (punto A):

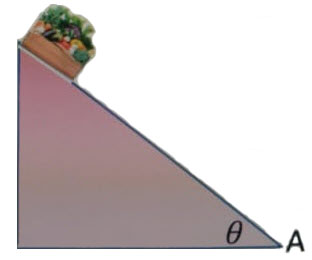
a) Dibuja el diagrama de cuerpo libre (DCL) de la caja en la posición inicial.

b) Escribe la segunda ley de Newton para la caja en las direcciones paralela y perpendicular a la rampa.

c) Encuentra el ángulo que forma la rampa con la horizontal.

d) Suponiendo ahora que el coeficiente de fricción cinética entre la rampa y la caja es , calcula la aceleración del bloque y su rapidez en la base de la rampa (punto A).

Un balde de pintura de 20 kg se encuentra en reposo sobre una rampa de la que se desconoce su inclinación. Se sabe que el coeficiente de fricción vale 1.20. Determina el ángulo de inclinación de la cuesta.

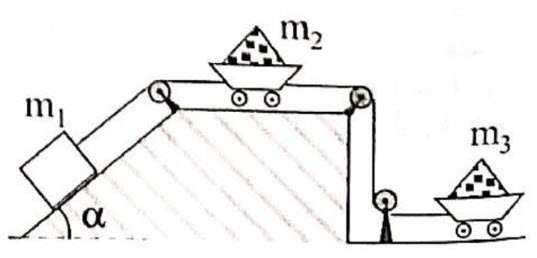
Dos carritos y son conectados mediante cables y poleas a un bloque . El coeficiente de rozamiento de y es y para el carrito es . La masa del bloque y de los carritos es la misma. ¿Cuál debe ser el ángulo del plano inclinado para que los carritos se muevan con una aceleración de ?

En la figura se muestra un bloque de 0.5 kg que cuelga de una cuerda. Los extremos de la cuerda están sujetos al techo en unos puntos separados 1.0 m. ¿Qué ángulo forma la cuerda con el techo?