En las figuras se representa la variación de la posición (y) de un punto de una cuerda vibrante en función del tiempo (t) y de su distancia (x) al origen, respectivamente.

a) Deduce la ecuación de onda.

b) Determina la velocidad de propagación de la onda y la velocidad de vibración de un punto de la cuerda.

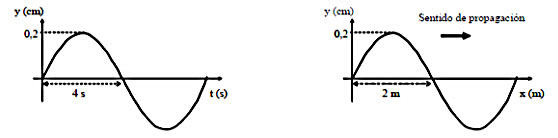
En un estadio el público se hace la ola para celebrar la buena actuación del equipo local. La ola es tan grande que dos espectadores de la misma fila separados por un mínimo de 50 m se mueven igual y lo hacen cada 10 s.

a) Si se ’’modelizase’’ esta ola en el estadio como una onda, ¿de qué tipo de onda se trataría? Calcula su longitud de onda y la pulsación (frecuencia angular).

b) Un espectador se mueve 1.0 m verticalmente cuando se levanta y se sienta al hacer la ola. Escribe la ecuación del movimiento de este espectador considerando que describe un movimiento armónico simple y que en el instante inicial está sentado, es decir, en su posición mínima.

c) Escribe la ecuación de ondas de la ola.

Si la onda en una cuerda tensa tiene una amplitud de 0.5 m , una frecuencia de 20 Hz y una velocidad de propagación de 10 m/s, escribe la ecuación de la onda.

Una onda armónica transversal se propaga en el sentido positivo del eje OX a 90 km/h, tiene una amplitud de 2 m y una frecuencia de 80 Hz. En el instante inicial, en un punto situado en x = 1.25 m, tiene una elongación máxima positiva. Determina lo siguiente: frecuencia angular, longitud de onda, número de onda, periodo, ecuación de onda para cuando t = 0.01 s.

Escribe la ecuación de una onda que se propaga en una cuerda (en sentido negativo del eje X) y que tiene las siguientes características: 0.5 m de amplitud, 250 Hz de frecuencia, 200 m/s de velocidad de propagación y la elongación inicial en el origen es nula. Determina la máxima velocidad trasversal de un punto de la cuerda.

Una onda que tiene una ecuacion, en unidades SI:

Pasa del medio en el que se propagan a otro donde su velocidad se duplica y su amplitud se reduce a la mitad. Escribe la ecuación de propagación de la onda en el segundo medio, considerando que la frecuencia permanece constante.

Una onda electromagnética plana, que está polarizada, tiene un campo eléctrico de amplitud 3 N/C y una frecuencia de 1 MHz.

a) Determina la ecuación de onda que representa al campo eléctrico si la onda se propaga en el eje Y, estando el campo polarizado en el eje Z.

b) Calcula la dirección de polarización del campo magnético.

Una onda transversal de 5 cm de amplitud y 25 Hz de frecuencia se propaga con una velocidad de 15 m/s por una cuerda tensa hacia la derecha.

a) Calcula la ecuación matemática de la onda.

b) Determina el primer instante en el que la velocidad de vibración de una partícula situada a 1 m del foco es máxima.

Una onda se propaga por la parte negativa del eje X con una longitud de onda de 20 cm, una frecuencia de 25 Hz, una amplitud de 3 cm y fase inicial igual a cero. Escribe la ecuación de la onda e indica el instante en el que un punto que se encuentra a 2.5 cm del origen alcanza, por primera vez, una velocidad nula.

Un vehículo de emergencias viaja hacia el este por una carretera con velocidad constante de 33.5 m/s. Sabiendo que su sirena emite el sonido con una frecuencia de 400 Hz. Calcula la frecuencia que escuchará una persona que viaja en coche hacia el oeste con velocidad constante de 24.6 m/s:

a) Cuando el coche se acerca al vehículo de emergencias.

b) Cuando el coche se aleja del vehículo de emergencias.