Ejercicios Resueltos de Vectores, Cinemática, Dinámica y Energía (2.º Bach)

Sabiendo que el vector de posición de una partícula es :

a) ¿Cuál es el vector velocidad?

b) ¿Cuál será la celeridad de la partícula cuando t = 2 s?

Encuentra el ángulo entre dos vectores de 10 y 15 unidades de longitud, cuando su resultante tiene 12 unidades de longitud.

Dos vectores se definen como y . Encuentra:

a)

b) El ángulo entre y

Calcula el desplazamiento resultante de la suma de los vectores y y exprésala en coordenadas polares.

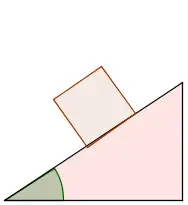
Calcula el trabajo realizado por las fuerzas que actúan sobre un cuerpo que desliza sobre un plano inclinado un ángulo como el que ves en la figura, sabiendo que su masa es 5 kg y el coeficiente de rozamiento dinámico es 0.2, cuando el cuerpo desciende 0.75 m por el plano:

Una partícula de masa m con rapidez impacta sobre un extremo de una barra de longitud L, que se encuentra en reposo y que puede girar libremente en torno al extremo opuesto al del impacto. Después del choque, la partícula queda incrustada en la barra y el sistema partícula-barra se detiene cuando el extremo del impacto alcanza una altura de L/2. Determina:

a) La velocidad angular de la barra un instante después del choque.

b) La velocidad de la partícula antes del choque.

Un jugador de baloncesto de 1.95 m de altura lanza un tiro a la canasta situada a 3.05 m de altura desde una distancia horizontal de 9.6 m. Si el ángulo de tiro es de con la horizontal, ¿con qué velocidad inicial debe tirar de manera que el balón entre al aro sin golpear el tablero?

Desde una altura de 80 m se lanza una piedra por encima de la horizontal, resultando que su alcance es de 80 m desde la base del lanzamiento, en un tiempo de 6 s. Calcula:

a) Ángulo del lanzamiento.

b) Vector velocidad inicial.

c) Dirección del vector velocidad y del vector aceleración a los 3 s del lanzamiento.

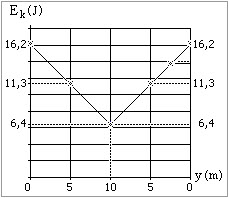
La gráfica representa la energía cinética en función de la posición vertical, para una partícula que sigue una trayectoria parabólica. De acuerdo con los datos suministrados, halla la masa de la partícula y la velocidad inicial y dirección de lanzamiento.

La posición de una partícula viene dada por el vector 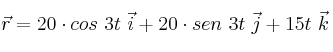. Calcula:

a) La velocidad media en el intervalo entre 1.3 y 1.6 s.

b) La velocidad instantánea en función del tiempo.

c) El vector velocidad para el instante 1.5 s.

d) La aceleración instantánea.