Una bala de 0.003 kg se mueve a 600 m/s en una dirección de sobre la horizontal. Calcula las componentes horizontal y vertical de la cantidad de movimiento de la bala.

Un cuerpo de masa 5 kg está comprimiendo a un resorte de constante elástica 5 000 N/m, una distancia inicial de 15 cm. Inicialmente el cuerpo A se encuentra en reposo y se suelta el resorte permitiendo que el mismo se desplace libremente por una superficie sin fricción hacia la derecha. El cuerpo A choca contra otro cuerpo B que está en reposo y cuya masa es de 8 kg, siendo la velocidad de B tras el choque de 3.5 m/s hacia la derecha. Determina:

a) La velocidad del cuerpo A después del choque.

b) El impulso que le aplica el cuerpo A al cuerpo B.

c) El impulso que le aplica el cuerpo B al cuerpo A.

Sobre un plano horizontal y liso se encuentran en reposo dos esferas de igual tamaño, pero masas distintas, unidas por una varilla. Se lanza un proyectil y este se incrusta en la masa más grande, como se ve en la figura:

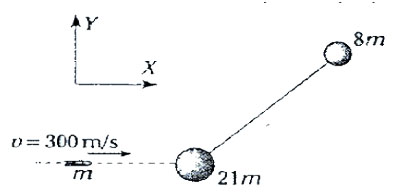
Determina la velocidad del centro de masas del sistema después del impacto. Desprecia el valor de la masa de la varilla y considera la velocidad del proyectil constante.

Cuando un coche esta cargado con 25 kg, su altura es de 25 cm. Si lo cargamos con 75 kg, su altura desciende a 20 cm. ¿Cuál es la constante elástica de los amortiguadores y cuál es la altura del coche cuando no está cargado?

A partir de la tabla de datos obtenida en el laboratorio, para la deformación de un muelle por acción del peso:

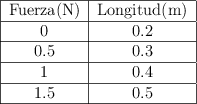
a) ¿Cuál es el valor de la constante recuperadora del muelle empleado?

b) ¿Qué fuerza habría que aplicar para que la deformación del muelle fuera de 15 cm?

c) ¿Qué longitud alcanzaría el muelle si colgamos un peso de 2.3 N?

Una persona de 70 kg que practica el deporte extremo conocido como puenting, salta al vacío desde un puente. La cuerda elástica que tiene amarrada a sus tobillos mide 10 m sin estirar. Suponiendo que se cumple la ley de Hooke, determina la constante de recuperación de la cuerda si la persona cae una distancia total de 30 m.

Sobre un cuerpo de 10 kg, en reposo en un plano horizontal, actúa una fuerza de 50 N. Se observa que en recorrer 50 m ha tardado 5 s. Determina:

a) El valor del coeficiente de rozamiento entre el cuerpo y el plano.

b) La velocidad del cuerpo al cabo de ese tiempo.

c) El trabajo realizado por la fuerza de rozamiento.

Dos masas están unidas por un hilo que pasa por una polea ligera con fricción insignificante, una masa está en un plano inclinado de sin fricción y otra masa cuelga libremente. Calcula la aceleración de las masas y la tensión de la cuerda.

Responde, de forma razonada, a las siguientes cuestiones:

a) Si el peso es un tipo de fuerza, ¿quiere decir que una persona obesa tiene mucha fuerza?

b) Si a una masa cualquiera le aplico una fuerza, ¿a qué será directamente proporcional esta?

En el sistema de la figura:

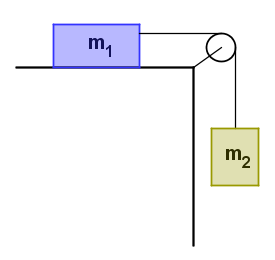
y . Sabiendo que el coeficiente de rozamiento del cuerpo 1 con el plano es de 0.40, ¿se mueve el sistema? ¿Con qué aceleración lo haría?