Ejercicios FyQ

Ejercicios Resueltos de Vectores, dimensiones y unidades

En mecánica, la fuerza «centrífuga» en un sistema rotatorio no inercial se expresa como:

$\vec{F}_{\text{centr}\acute{\imath}\text{fuga}} = m \cdot \vec{\omega} \times (\vec{\omega} \times \vec{r})$

donde: «m» es la masa de la partícula (en kg), « $\vec{\omega}$ » es la velocidad angular y « $\vec{r}$ » es el vector de posición, todas la magnitudes expresadas en unidades SI.

a) Determina las dimensiones de la fuerza «centrífuga» y verifica que coincidan con las de una fuerza.

b) Si $\omega = 2\ \text{rad}\cdot s^{-1}$ y r = 0.5 m, calcula el módulo de la fuerza «centrífuga» para una masa de 3 kg.

Solución

Transforma las siguientes coordenadas polares a coordenadas rectangulares: B (5 km; $530 ^o$ al oeste) a B (x, y).

Solución

Determina la ecuación de dimensiones del momento de inercia y comprueba la homogeneidad de las siguientes fórmulas físicas:

a) $N=I\cdot \alpha$

b) $N\cdot t = \Delta (I\cdot \omega)$

c) $N\cdot \phi = \Delta \left(\frac{1}{2}\cdot I\cdot \omega^2\right)$

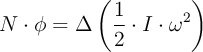
donde «N» es el momento del par, «I» es el momento de inercia, «t» es el tiempo y « $\phi$ », « $\omega$ » y « $\alpha$ » son, respectivamente, el ángulo de giro, la velocidad angular y la aceleración angular.

Solución

Determina la ecuación dimensional y las unidades SI del coeficiente de viscosidad y el número de Reynolds.

Solución

Para los siguientes vectores: $\vec A = (4, -1, -6)$ ; $\vec B = (5, 7, -2)$ ; $\vec C = (-8, -5, 2)$ y $\vec D = (9, -4, 0)$ , determina:

a) $(\vec A + \vec B)$ ; $(\vec A - \vec B)$ ; $(\vec D + \vec C)$ ; $(\vec A - \vec D)$ .

b) La magnitud de cada vector y los ángulos que forman con los ejes x , y , z.

c) Los productos escalares: $\vec A\cdot \vec B$ ; $\vec D\cdot \vec C$ ; $\vec B\cdot \vec C$ ; $\vec B\cdot \vec D$ .

d) Los productos vectoriales: $\vec A\times \vec B$ ; $\vec D\times \vec C$ ; $\vec B\times \vec C$ ; $\vec B\times \vec D$

Solución

Dado el vector $\vec A = 4\vec i + 5\vec j - 2\vec k$ y conociendo que el módulo de B = 10 m y que sus ángulos directores son $\alpha = 60 ^o$ , $\beta > 90 ^o$ y $\gamma = 120 ^o$ , determina el ángulo que forman el vector (A - B) con el vector B.

Solución

Se dan los siguientes vectores $\vec A = 3\vec i - \vec j - 4\ \vec k$ , $\vec B = -2\ \vec i + 4\ \vec j - 3\ \vec k$ y $C = \vec i + 2\ \vec j - \vec k$ . Halla un vector unitario en la dirección del vector $3\vec A - 2\vec B +4\vec C$ .

Índice de Ejercicios RESUELTOS