-
Conservación de la cantidad de movimiento en un sistema de partículas (7457)
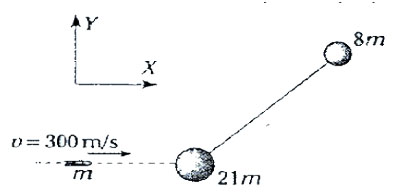
Sobre un plano horizontal y liso se encuentran en reposo dos esferas de igual tamaño, pero masas distintas, unidas por una varilla. Se lanza un proyectil y este se incrusta en la masa más grande, como se ve en la figura:
Cantidad movimiento
Determina la velocidad del centro de masas del sistema después del impacto. Desprecia el valor de la masa de la varilla y considera la velocidad del proyectil constante.
-
Ampliación: composición de movimientos y conservación del momento lineal y energía mecánica (7441)
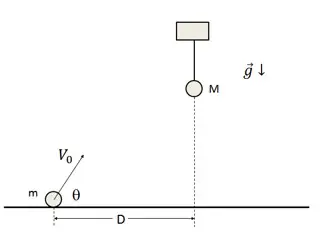
En la figura se aprecia un proyectil de masa m = 0.6 kg que se lanza desde el suelo con una rapidez inicial 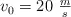 y un ángulo
y un ángulo 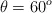 con respecto a la horizontal. El proyectil impacta a un cuerpo de masa M = 0.2 kg colgado en una cuerda justo en el instante en que alcanza su máxima altura. El choque entre el proyectil y el cuerpo es plástico, y ambos cuerpos pegados se elevan lateralmente hasta detenerse.
con respecto a la horizontal. El proyectil impacta a un cuerpo de masa M = 0.2 kg colgado en una cuerda justo en el instante en que alcanza su máxima altura. El choque entre el proyectil y el cuerpo es plástico, y ambos cuerpos pegados se elevan lateralmente hasta detenerse.
a) Determina la distancia D entre la posición de lanzamiento del proyectil y la posición horizontal del cuerpo.
b) Determina la velocidad de los dos cuerpos pegados inmediatamente después del choque.
c) Determina la máxima altura con respecto al suelo que alcanzan los dos cuerpos pegados después del choque.
Cantidad movimiento
-
Conservación de la energía mecánica y del momento lineal (7300)
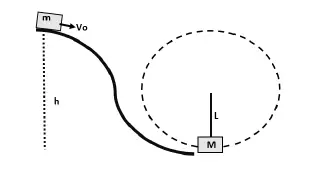
Una partícula de masa m se lanza con una velocidad inicial 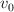 desde una altura h. Si en el trayecto AB se degrada una cantidad de energía igual a
desde una altura h. Si en el trayecto AB se degrada una cantidad de energía igual a 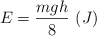 y si m choca de forma perfectamente inelástica con M, determina la
y si m choca de forma perfectamente inelástica con M, determina la 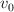 mínima de m para que las partículas describan un movimiento circular.
mínima de m para que las partículas describan un movimiento circular.
Cantidad movimiento
-
Velocidad del tercer fragmento de un explosivo que estalla (7298)
Se sabe que una bomba de 20 kg estalló en tres fragmentos, de los cuales dos salieron con velocidades 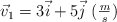 y
y 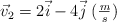 y masas
y masas 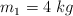 y
y 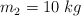 . Si había una persona en la posición (-6,1) (m), ¿fue impactada por el tercer fragmento de la bomba?
. Si había una persona en la posición (-6,1) (m), ¿fue impactada por el tercer fragmento de la bomba?
-
Velocidad que adquiere un cosmonauta al empujar una bomba en el espacio (7111)
Durante una reparación en la estación espacial internacional, un cosmonauta de masa de 75 kg reemplaza una bomba dañada del sistema de refrigeración de 420 kg. Inicialmente, el cosmonauta y la bomba están en reposo en relación con la estación. Cuando empuja la bomba al espacio, él se desplaza en la dirección opuesta. En este proceso, la bomba adquiere una velocidad de 0.7 m/s desde la estación. ¿Cuál es el valor de la velocidad escalar adquirida por el cosmonauta en relación con la estación después del empuje?
 Cantidad movimiento
Cantidad movimiento