Una fuerza de 80 N paralela a un plano inclinado (sobre el eje x) tira de una de masa de 10 kg hacia abajo con una fuerza de fricción de 20 N y con un ángulo de . Determina la aceleración y la velocidad final, suponiendo que parte del reposo, cuando ha recorrido 4 m.

Colocamos un cuerpo en lo alto de un plano inclinado que tiene un ángulo de con la horizontal. Si el coeficiente de rozamiento cinético es 0.2, ¿con qué aceleración desliza por el plano?

Un coche de 1 100 kg circula a una velocidad de 80 km/h y ve una señal de «Stop» a 150 m. Comienza a reducir la marcha en ese instante y se detiene en 18 s. Calcula la aceleración de frenada y la fuerza ejercida por los frenos.

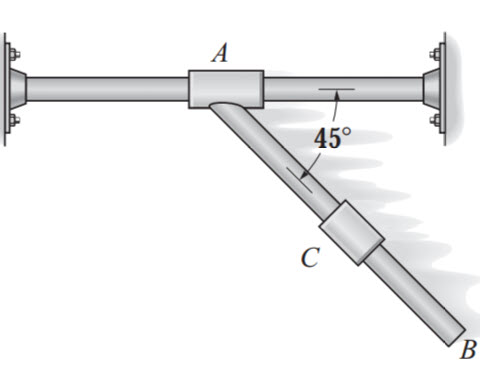
El anillo «C», de 2 kg de masa, se desliza libremente a lo largo del tramo liso AB. Determina la aceleración del anillo si:

a) El anillo «A» está fijo y no se mueve el tramo AB.

b) El anillo «A» se mueve hacia la izquierda con velocidad constante a lo largo de la guía horizontal.

c) El anillo «A» se somete a una aceleración de hacia la izquierda.

Considera que en todos los casos el movimiento ocurre en el plano vertical.

La imagen presenta dos masas y unidas por una cuerda que pasa por una polea sin fricción y masa despreciable. La masa se encuentra sobre una superficie rugosa.

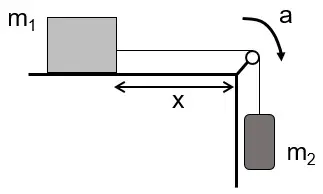
a) Realiza un diagrama de fuerzas para cada masa.

b) Expresa la aceleración del sistema en términos de las masas y el coeficiente de fricción cinética .

c) Halla el valor de la aceleración, tomando como valor .

d) Si el bloque se encuentra a una distancia x = 0.961 m, ¿cuánto tardará en llegar a la esquina de la mesa?

e) ¿Cuál debería ser la masa mínima de para que el sistema quede en reposo? Toma el valor del coeficiente de fricción estático como .

Calcula la aceleración que sufre un cuerpo de 20 kg cuando se le aplica una fuerza constante de 185 N.

Sobre un cuerpo de 30 kg, que está en un plano horizontal, se aplica una fuerza de 100 N que forma un ángulo de con la horizontal. Sabiendo que el coeficiente de rozamiento cinético es 0.2, ¿cuál es la aceleración que sufre el cuerpo?

Un objeto de 200 g de masa se ve sometido a dos fuerzas de 5 N. Calcula la aceleración de dicha masa cuando las fuerzas son de la misma dirección y sentido.

Un objeto de 100 kg, se encuentra sobre un plano horizontal. Si tiramos de él con una fuerza de 300 N, el coeficiente de rozamiento es 0.1 y recorre una distancia de 6 m:

a) ¿Con qué aceleración se moverá?

b) Encuentra el trabajo que realiza cada fuerza que actúa sobre el bloque.

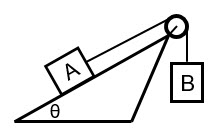
Calcula la aceleración del sistema de la figura, en función de la aceleración de la gravedad y en ausencia de rozamiento, sabiendo que y .