Un electrón se esta moviendo horizontalmente con una energía cinética de y entra en una región de un campo eléctrico cuyo valor es de y que apunta hacia abajo. Si esa región mide horizontalmente 1 cm, determina el ángulo con el que el electrón deja esa región, medido con respecto a su trayectoria original.

En un sistema bidimensional colocamos dos cargas distantes 3 metros a lo largo de una dimensión; y .

Obtén el campo eléctrico en un punto P, a una altura de 5 metros sobre la carga utilizando el Principio de Superposición para ello.

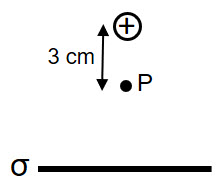
Considere el sistema dado por un plano infinito uniformemente cargado y una partícula con una carga . Si el campo eléctrico resultante en el punto P es vertical hacia abajo y tiene módulo de :

a) Determina el campo eléctrico generado por el plano y su densidad superficial de carga.

b) Determina la posición donde el campo eléctrico resultante es nulo.

Dato: ;

Una partícula de masa parte del reposo a 3 cm de una placa infinita uniformemente cargada y con densidad superficial de carga . Se sabe que y que la partícula llega a la placa negativa con una velocidad .

a) Determina y representa el campo eléctrico resultante entre las placas.

b) Determina y representa la fuerza eléctrica que actúa sobre la partícula.

c) Determina el valor y signo de la carga eléctrica de la partícula.

Dato: .

Sea una línea de carga infinita uniformemente cargada de densidad lineal de carga , siendo q la carga que hay en un largo L de la línea de carga.

a) Muestra que el campo eléctrico generado por la línea de carga es perpendicular a la misma en cualquier punto del espacio e indica qué tipo de simetría posee el campo eléctrico generado por la misma.

b) Demuestra, a partir de la ley de Gauss, que el campo eléctrico generado por la línea de carga en un punto cualquiera a una distancia r de la misma esta dado por la ecuación .

Tres cargas eléctricas , y , se encuentran en los vértices de un triángulo equilátero de lado 20 cm. En el punto medio entre las cargas y (justo debajo de la carga ), se quiere estudiar el campo total que actúa allí, con una carga de prueba P de valor insignificante.

a) Realiza el diagrama de cargas y coloca las fuerzas eléctricas.

b) ¿Cómo son los campos eléctricos de las cargas en función de la carga de prueba P y cuales son sus valores?

c) ¿Cuánto vale el campo eléctrico total sobre el punto donde se encuentra P y hacia donde se dirige el mismo?

Dos cargas y de valor desconocido se encuentran separadas 0.20 m. El campo eléctrico en el punto 0 (equidistante a las cargas) es .

a) Determina el campo creado por en el punto 0.

b) Determina el valor y signo de .

c) Determina el potencial eléctrico en el punto 0.

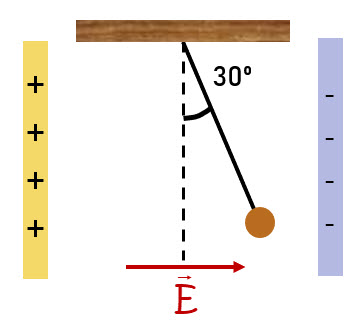
El campo eléctrico entre las placas de un condensador vale 4 000 N/C. ¿Cuánto vale la carga de la esfera si su masa es de 3 g y el hilo que sujeta a la esfera forma un ángulo de con la vertical?

El flujo eléctrico total que pasa por una superficie cerrada en la forma de un cilindro es de , calcula:

a) La carga neta dentro del cilindro.

b) El flujo eléctrico para una carga neta dentro del cilindro igual a .

El campo electrostático creado por una carga puntual q situada en el origen de coordenadas, viene dado por la expresión:

donde r se expresa en metros y es un vector unitario dirigido en la dirección radial. Si el trabajo realizado para llevar una carga desde un punto A a otro B que distan del origen 5 y 10 m respectivamente, es de , determina:

a) El valor de la carga puntual q que está situada en el origen de coordenadas.

b) El valor de la carga que se ha transportado desde A hasta B.

Dato: