Dos conductores a y b rectos y largos se colocan en forma paralela, tal como indica la figura. Si la intensidad del conductor en el conductor a es de 8.0 A y el campo magnético resultante en el punto P es nulo:

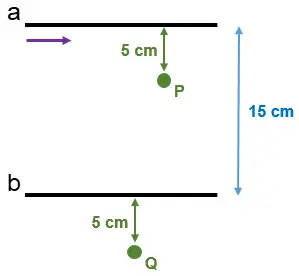
a) Determina la intensidad de corriente en el conductor b e indica el sentido de la corriente.

b) Determina el campo magnético resultante en el punto Q.

Un protón se mueve con una velocidad de a lo largo del eje X. Entra en un campo magnético de 1.7 T cuya dirección forma un ángulo de con la velocidad. Calcula la fuerza que experimenta el protón y la aceleración que adquiere.

Datos: ;

Un electrón se mueve a una velocidad , como se muestra en la figura. Calcula el campo magnético que produce en los puntos A, B y C, sabiendo que todos están a una de distancia del electrón.

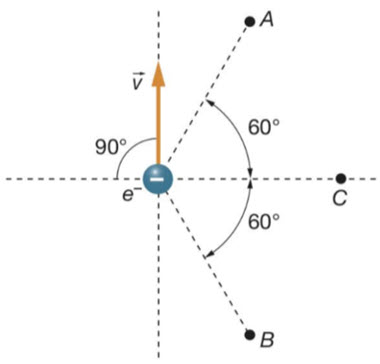
Datos: ;

Un espira tiene un radio de 5 cm. Si circula por ella una corriente de 3.5 A en sentido contrario a las agujas del reloj, ¿cuánto vale el campo magnético en el centro de la espira? La espira está colocada en el plano XY.

Dato: .

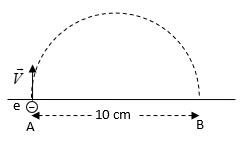
Un electrón tiene en el punto A de la figura una velocidad de en el sentido indicado. De acuerdo a los datos que aparecen:

a) Señala la dirección y sentido de las líneas del campo magnético uniforme que debe extenderse por encima del plano AB.

b) Calcula el valor de la intensidad del campo magnético que obligará al electrón a seguir la trayectoria semicircular de A hasta B.

c) ¿Qué tiempo demora la partícula en moverse desde A hasta B?

Datos: ;

Un hilo conductor recto e indefinido es atravesado por una corriente de 12 A. Calcula el valor del campo magnético que produce en un punto situado a 7 mm del conductor y representa el vector del campo.
Dato:

Calcula el valor de un campo magnético uniforme si se coloca dentro de él un alambre conductor perpendicular a las líneas del campo que tiene 8 cm de largo y experimenta una fuerza de , cuando circula una corriente de 5 A.

Una partícula de masa y carga 10 nC ingresa a una región de campo magnético uniforme, perpendicular al plano, con velocidad . En dicha región describe una semicircunferencia de radio R = 4.0 mm. Determina el campo magnético en la región.

Dos espiras circulares concéntricas de radios de 20 cm y 9 cm están en un mismo plano. Por ellas circula una corriente de 30 A y en sentidos opuestos. ¿Cuál es el valor del campo magnético resultante en el centro de las espiras?

Dos conductores rectilíneos están separados 4 cm uno del otro. Por el primero de ellos circula una corriente de 2 A y por el segundo una corriente de 2.8 A. Calcula el campo magnético resultante en un punto situado a 1.9 cm del primer conductor:

a) Cuando las corrientes son en el mismo sentido.

b) Cuando las corrientes son de sentido contrario.