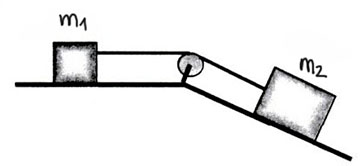
La figura muestra una masa de ![]() que descansa sobre una superficie horizontal lisa y que está unida a otra masa
que descansa sobre una superficie horizontal lisa y que está unida a otra masa ![]() que se encuentra sobre un plano inclinado liso, que forma un ángulo de
que se encuentra sobre un plano inclinado liso, que forma un ángulo de ![]() con la horizontal. Ambas masas se unen por medio de una cuerda ideal y que pasa por una polea de radio
con la horizontal. Ambas masas se unen por medio de una cuerda ideal y que pasa por una polea de radio ![]() . La cuerda no desliza sobre la polea, que puede girar libremente alrededor de un eje perpendicular a la página y que pasa por su centro. Cuando el sistema se libera del reposo, la masa
. La cuerda no desliza sobre la polea, que puede girar libremente alrededor de un eje perpendicular a la página y que pasa por su centro. Cuando el sistema se libera del reposo, la masa ![]() se mueve hacia la derecha con una aceleración
se mueve hacia la derecha con una aceleración ![]() . ¿Cuál es la inercia rotacional de la polea?
. ¿Cuál es la inercia rotacional de la polea?
En un partido amistoso de fútbol entre Argentina y Brasil, cuando estaban empatados a uno y en el minuto 90, el árbitro pita una falta a favor de Brasil alejada 32 m de la portería. El jugador que la lanza es capaz de imprimir una velocidad de 30 m/s a la pelota y la barrera de los jugadores argentinos, de una altura media de 1.80 m, se sitúa a 12 m del punto de lanzamiento. Determina:
a) ¿Cuál debe ser el ángulo del lanzamiento para colocar el balón en la esquina superior izquierda sin que la barrera obstruya el lanzamiento?
b) ¿Cuál debe ser el ángulo del lanzamiento para colocar el balón en la esquina inferior izquierda sin que la barrera obstruya el lanzamiento?
La fuerza ejercida sobre un automóvil por una barrera parachoques al golpear el automóvil contra ésta es ![]() , donde s es la distancia en pies medida desde el punto de contacto inicial. Si se quiere diseñar la barrera de manera que pueda detener un auto de
, donde s es la distancia en pies medida desde el punto de contacto inicial. Si se quiere diseñar la barrera de manera que pueda detener un auto de ![]() que viaje a
que viaje a ![]() , ¿cuál será la longitud efectiva necesaria de la barrera, es decir, cuál será la distancia necesaria de la barrera para que detenga al automóvil?
, ¿cuál será la longitud efectiva necesaria de la barrera, es decir, cuál será la distancia necesaria de la barrera para que detenga al automóvil?
El módulo de Young para la resilina, una proteína flexible parecida al caucho encontrada en artrópodos, se determinó mediante experimentos con el tendón elástico del caballito del diablo. El tendón tenía inicialmente 0.72 mm de longitud y 0.13 mm de diámetro, encontrándose que una carga de 2.4 g lo alargaba hasta una longitud de 1.39 mm. A partir de estos datos, calcula el módulo de Young.
Una rueda de caballitos tiene un momento de inercia ![]() y gira alrededor de su eje vertical a
y gira alrededor de su eje vertical a ![]() . En su borde, que dista 1.40 m del eje, está sentado un muchacho de m = 60.0 kg. Calcula el momento angular del sistema rueda-muchacho.
. En su borde, que dista 1.40 m del eje, está sentado un muchacho de m = 60.0 kg. Calcula el momento angular del sistema rueda-muchacho.
Dos masas puntuales ![]() y
y ![]() están separadas por una barra sin masa de longitud L:
están separadas por una barra sin masa de longitud L:
a) Deduce una expresión para el momento de inercia del sistema, respecto a un eje perpendicular a la barra y que pasa por un punto situado a una distancia ![]() de la masa
de la masa ![]() .
.
b) Calcula la variación del momento angular con la distancia y demuestra que es mínima cuando el eje pasa por el centro de masas del sistema.
Un sistema natural se puede modelar con un conjunto de figuras geométricas que consiste en una esfera de radio ![]() y densidad
y densidad ![]() , un cilindro de radio
, un cilindro de radio ![]() y altura
y altura ![]() y dos esferas idénticas de radio
y dos esferas idénticas de radio ![]() , siendo la densidad de estas tres últimas figuras geométricas
, siendo la densidad de estas tres últimas figuras geométricas ![]() :
:
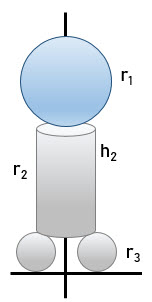
¿Cuál es la posición del centro de masas del sistema, respecto a los ejes de coordenadas sobre los que está representado?
Encuentra el centro de masas del sistema formado por las siguientes partículas, dadas sus masas y sus coordenadas expresadas en metros: ![]() ;
; ![]() ;
; ![]() y
y ![]() . Realiza un dibujo en el que aparezcan las masas representadas como un punto y el centro de masas con una equis.
. Realiza un dibujo en el que aparezcan las masas representadas como un punto y el centro de masas con una equis.
Dos masas de 5 kg y 9 kg están localizadas en posiciones (5, 0, 0) y (7, 0, 0) respectivamente, en metros, a partir del origen. ¿Dónde se sitúa el centro de masas del sistema?
La masa de la Tierra es 81 veces mayor que la de la Luna y la distancia entre sus centros es sesenta radios terrestres (60 R). El centro de masas del sistema Tierra-Luna ocupa una posición que está:
a) Por encima de la superficie terrestre.
b) Por debajo de la superficie terrestre.
c) A la mitad de la distancia entre ambos cuerpos celestes.
d) Indeterminada, ya que depende de las fases de la Luna.
 Ejercicios FyQ
Ejercicios FyQ