Tres cargas puntuales de valores +q, +2q y -4q están fijas en los vértices de un triángulo equilátero de lado d = 10 cm, como se muestra en la figura. La energía potencial electrostática del conjunto de las tres cargas es igual a . La constante de la ley de Coulomb es .

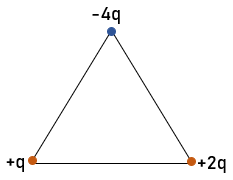
Calcula:

a) El valor de la carga q.

b) El potencial en el punto medio del segmento que une las dos cargas positivas.

c) El módulo y dirección del campo eléctrico en el punto medio del segmento que une las dos cargas positivas. Indica la dirección y sentido mediante un diagrama.

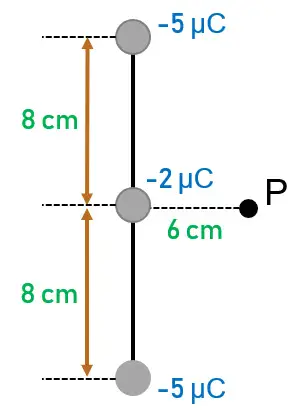
Tres cargas puntuales negativas están sobre una línea, como se ilustra en la figura. Encuentra la magnitud y la dirección que produce esta combinación de cargas en el punto P, que está a 6 cm de la carga de medido en forma perpendicular a la línea que conecta las tres cargas.

Un acelerador lineal de partículas lanza un protón (carga +e) directamente hacia un núcleo de helio (carga +2e), que permanece en reposo en todo momento. La velocidad inicial del protón es de y la distancia inicial entre las partículas es muy grande, considerándose su interacción eléctrica en ese momento nula.

a) Calcula la separación mínima entre las partículas justo antes de que comiencen a separarse de nuevo.

b) Calcula el valor máximo de la aceleración del protón en su interacción con el núcleo de helio.

Datos: ;

Una carga de y una carga de se separan una distancia de 50 cm. Determina la posición en la que se puede colocar una tercera carga de de modo que la fuerza electrostática neta sobre ella sea cero.

a) Enuncia la ley de Coulomb y comenta su expresión.

b) Dos cargas puntuales q y –q se encuentran sobre el eje X, en x = a y en x = -a, respectivamente. Escribe las expresiones del campo electrostático y del potencial electrostático en el origen de coordenadas.

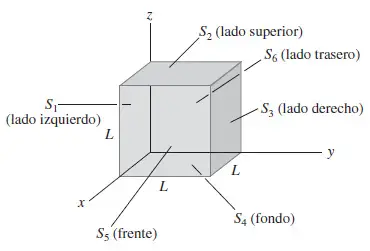
El cubo de la figura tiene los lados de longitud L = 10.0 cm y el campo eléctrico uniforme tiene un módulo de , siendo paralelo al plano XY y formando un ángulo de a partir del eje +X y hacia el eje +Y.

a) ¿Cuál es el flujo a través de cada una de las seis caras del cubo?

b) ¿Cuál es el flujo eléctrico total a través de todas las caras del cubo?

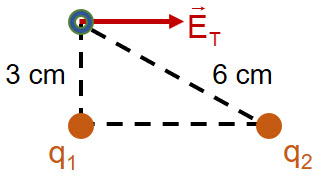
En dos vértices de un triángulo rectángulo se ubican las partículas con cargas y , tal como muestra la figura. En el vértice libre se ha representado el campo eléctrico total , cuyo valor es , siendo paralelo a la recta que une a las dos partículas. Determina el valor y el signo de cada una de las cargas y .

En el interior de una superficie gaussiana de forma irregular se encuentran tres partículas cargadas, tal como se ve en la figura. Se sabe que .

a) Sabiendo que el flujo del campo eléctrico a través de la superficie gaussiana es de , determina el valor y el signo de .

b) ¿Qué valor y signo deberá tener la tercera carga si el flujo del campo eléctrico a través de la superficie es nulo?

.

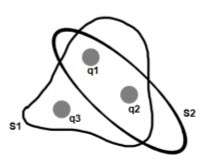
Las tres partículas cargadas que se encuentran en el dibujo adjunto se encuentran a 3.0 cm del punto P. Se sabe que las cargas de las partículas 1 y 2 son iguales, esto es, y que el campo eléctrico resultante de las tres partículas es nulo en dicho punto.

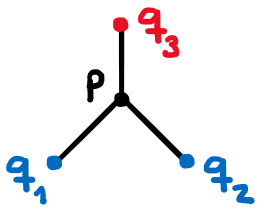
a) Encuentra el campo eléctrico resultante de las partículas 1 y 2.

b) Calcula valor y signo de la carga eléctrica de la tercera partícula.

Dos cargas y están situadas en el vacío a una distancia de 2 m. Calcula la variación de la energía potencial y el trabajo realizado para separarlas hasta una distancia de 4 m. Interpreta el signo del resultado obtenido.