Ejercicios FyQ
Un proyectil de 180 g se dispara contra un bloque de madera de 5 kg que inicialmente está en reposo. El proyectil que impacta a una velocidad de 150 m/s queda incrustado dentro del bloque.
a) ¿Qué altura máxima será la que ascienda el péndulo?
b) Si la longitud de la cuerda es de 1.3 m, ¿cuál será el ángulo que forme con la vertical?
Un hombre sobre un vagón abierto de ferrocarril que viaja con rapidez constante de 
, quiere lanzar una pelota a través de un aro estacionario a 4.90 m sobre la altura de la mano, de modo que la bola se mueva horizontalmente al pasar por el aro. El hombre lanza la bola con una rapidez de 
con respecto a sí mismo:
a) ¿Qué componente vertical debe tener la velocidad inicial de la bola?
b) ¿Cuántos segundos después del lanzamiento la bola atravesará el aro?
c) ¿A qué distancia horizontal del aro se deberá soltar la bola?
d) Cuando la pelota sale de la mano del hombre, ¿qué dirección tiene su velocidad relativa al marco de referencia del vagón? ¿Y relativa al marco de referencia de un observador parado en el suelo?
Se dispara un proyectil de 20 g contra un bloque de 2.5 kg que se encuentra en reposo en una mesa de 1 m de altura. El coeficiente de rozamiento entre el bloque y la mesa es 0.3. El proyectil se incrusta dentro del bloque y, después del impacto, el bloque se desplaza 10 cm sobre la mesa antes de caer y aterrizar a una distancia de 2 m de la parte inferior de la mesa. Determina la rapidez de la bala.
Un cuerpo se desliza a lo largo de un plano inclinado un ángulo de 
y luego continúa moviéndose sobre un plano horizontal la misma distancia que en el plano inclinado hasta detenerse. Calcula el coeficiente de fricción del trayecto mencionado.
Un objeto de 20 kg de masa, que parte del reposo desde lo alto de un plano inclinado de 3 m de alto y 4 m de base, llega a la parte inferior de este con una velocidad de 4 m/s. Calcula la fuerza de fricción y el coeficiente de rozamiento entre el plano inclinado y el objeto.
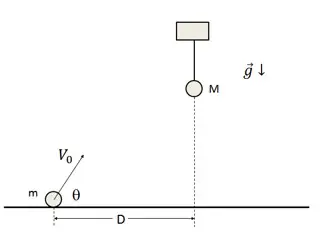
En la figura se aprecia un proyectil de masa m = 0.6 kg que se lanza desde el suelo con una rapidez inicial 
y un ángulo 
con respecto a la horizontal. El proyectil impacta a un cuerpo de masa M = 0.2 kg colgado en una cuerda justo en el instante en que alcanza su máxima altura. El choque entre el proyectil y el cuerpo es plástico, y ambos cuerpos pegados se elevan lateralmente hasta detenerse.
a) Determina la distancia D entre la posición de lanzamiento del proyectil y la posición horizontal del cuerpo.
b) Determina la velocidad de los dos cuerpos pegados inmediatamente después del choque.
c) Determina la máxima altura con respecto al suelo que alcanzan los dos cuerpos pegados después del choque.
Un objeto de masa m se libera sin velocidad inicial en una rampa de modo que desliza hacia abajo. La rampa es de longitud L , con coeficiente de rozamiento 
y tiene un ángulo de inclinación 
con respecto a la horizontal. Una vez que el objeto llega a la base de la rampa, sigue deslizándose por una superficie horizontal sin rozamiento, hasta tomar contacto con un resorte de constante elástica k y comprimirlo, tras lo que el resorte se expande e impulsa al objeto de vuelta hacia la rampa.
a) Encuentra una expresión para la velocidad del objeto al llegar a la base de la rampa.
b) Evalúa la expresión obtenida en el punto anterior considerando los siguientes datos:
m = 15 kg ; L = 7 m ; 
; 
; 
c) Con los datos y el resultado de b), determina la deformación máxima que experimenta el resorte.
d) Con los datos y resultados de los tres apartados primeros determina la máxima altura con respecto a la horizontal que alcanza el objeto en la rampa al detenerse después de ser impulsado por el resorte
Un muelle varía su longitud natural de 1.5 m (longitud en reposo) por la acción de la rotación de una masa 1 kg pegada a ella. Supón que no hay fricción, que la velocidad angular es 
y que la constante del muelle tiene un valor de 
.
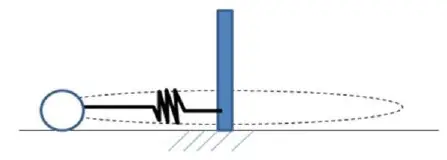
a) Calcula la elongación (
) que sufre el muelle. ¿Cuál será la nueva longitud del muelle?
b) Calcula la fuerza centrípeta, la aceleración normal y la fuerza normal.
c) Calcula el valor de una fuerza F en la dirección radial si se pretende disminuir la velocidad angular en un 
y se observa que la elongación del muelle es la mitad que en el primer apartado.
Los alimentos que comemos sufren un proceso de degradación en nuestro organismo por el que proporcionan la energía necesaria para el crecimiento y las funciones vitales. La ecuación de combustión de la glucosa es la que mejor describe el proceso:
Si la cantidad de alimentos que una persona consume al día equivale a una ingesta de 856 g de glucosa, calcula:
a) La masa de 
que se produce como consecuencia de la combustión de tal cantidad de glucosa.
b) La energía que se suministra al organismo.
c) El volumen de aire, medido a 
y 770 torr, que se necesita para la total combustión de la cantidad de glucosa indicada. Considera que el aire contiene un 
en volumen de oxígeno.
Datos: 
; 
; 
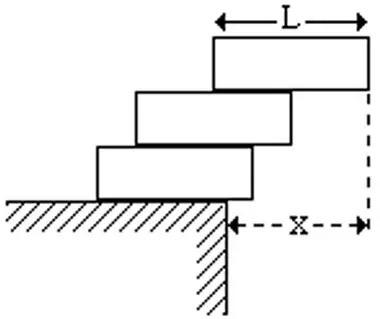
Los tres bloques de densidad uniforme y longitud 18 cm, se colocaron uno sobre el otro, en el borde de una superficie horizontal, sobresaliendo lo máximo posible y manteniendo el equilibrio. Halla la distancia horizontal x indicada en la figura:
