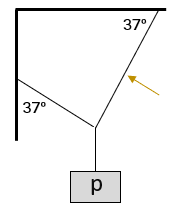
Una escopeta dispara muchos perdigones hacia arriba. Algunos viajan casi verticalmente, pero otros se desvían hasta ![]() de la vertical. Supón que la rapidez inicial de todos los perdigones es uniforme e igual a 150 m/s e ignora la resistencia del aire.
de la vertical. Supón que la rapidez inicial de todos los perdigones es uniforme e igual a 150 m/s e ignora la resistencia del aire.
a) ¿En qué radio del punto de disparo caerán los perdigones?
b) Si hay 1000 perdigones y se distribuyen uniformemente en el círculo del radio calculado en el inciso anterior, ¿qué probabilidad hay de que al menos un perdigón caiga en la cabeza de quien dispara? (Suponga que la cabeza tiene 10 cm de radio.).
c) En realidad, la resistencia del aire tiene varios efectos: frena los perdigones al subir, reduce la componente horizontal de su velocidad y limita la rapidez con que caen. ¿Cuál de esos efectos tenderá a hacer el radio mayor que el calculado en a) y cuál tenderá a reducirlo? ¿Qué efecto global cree que tendrá la resistencia? (Su efecto sobre una componente de velocidad se incrementa al aumentar la magnitud de la componente).
Una muestra de sangre se coloca en una centrifugadora de 15.0 cm de radio. La masa de una célula roja en la sangre es ![]() y la magnitud de la fuerza que actúa sobre ella para que se sedimente en el plasma es
y la magnitud de la fuerza que actúa sobre ella para que se sedimente en el plasma es ![]() . ¿Cuántas revoluciones por segundo debe alcanzar la centrifugadora?
. ¿Cuántas revoluciones por segundo debe alcanzar la centrifugadora?
Al lanzar un cuerpo de 2 kg con un ángulo de ![]() con la horizontal, se realiza un trabajo de 225 J. ¿Cuál es el tiempo que el cuerpo está en el aire antes de volver a tocar el suelo?
con la horizontal, se realiza un trabajo de 225 J. ¿Cuál es el tiempo que el cuerpo está en el aire antes de volver a tocar el suelo?
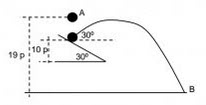
Un cuerpo cae desde una altura de 19 pies con respecto al piso. A una altura de 10 pies éste choca elásticamente contra un plano inclinado de ![]() con respecto a la horizontal. Encuentra el tiempo que emplea el cuerpo en tocar el piso desde que es soltado en el punto A.
con respecto a la horizontal. Encuentra el tiempo que emplea el cuerpo en tocar el piso desde que es soltado en el punto A.
Un electrón, que se desplaza con un velocidad de ![]() , se dispara contra una hoja de papel de espesor
, se dispara contra una hoja de papel de espesor ![]() . El electrón sale de la hoja con una velocidad de
. El electrón sale de la hoja con una velocidad de ![]() . Determina el tiempo que tarda el electrón al atravesar la hoja.
. Determina el tiempo que tarda el electrón al atravesar la hoja.
En el laboratorio se encuentra una disolución de ácido nítrico cuya concentración es desconocida. Para valorarla, una alumna tomó una alícuota de 20.00 mL en pipeta volumétrica y la diluyó hasta 250 mL en un matraz aforado, rotulándolo como disolución de trabajo. Paso seguido tomó alícuotas de 10.00 mL en pipeta volumétrica por triplicado y las tituló con una disolución de hidróxido de potasio 0.1375 M empleando una bureta, obteniendo los siguientes resultados: muestra A = 9.05 mL, muestra B = 9.10 mL y muestra C = 9.15 mL. A partir de estos resultados, calcula las concentraciones de la disolución de trabajo y la de concentración desconocida.
Desde la máxima altura de una montaña rusa (90 m), se desliza un carro que pesa 1 200 N. Mientras desciende se transforma el ![]() de la energía potencial en energía calórica debido al rozamiento y ha avanzado 40 m horizontalmente cuando llega a la parte más baja de la montaña rusa. Debido a la construcción de la montaña rusa el carro se desliza horizontalmente durante 30 m, transformando en esa distancia el
de la energía potencial en energía calórica debido al rozamiento y ha avanzado 40 m horizontalmente cuando llega a la parte más baja de la montaña rusa. Debido a la construcción de la montaña rusa el carro se desliza horizontalmente durante 30 m, transformando en esa distancia el ![]() de la energía cinética con la que había llegado a la parte más baja en energía calórica. Debido a la energía cinética que aún posee el carro, y a la construcción de la montaña rusa, inicia un ascenso recorriendo 67 m hasta llegar a la parte más alta de su segunda joroba, pero durante el ascenso, y debido al rozamiento, el
de la energía cinética con la que había llegado a la parte más baja en energía calórica. Debido a la energía cinética que aún posee el carro, y a la construcción de la montaña rusa, inicia un ascenso recorriendo 67 m hasta llegar a la parte más alta de su segunda joroba, pero durante el ascenso, y debido al rozamiento, el ![]() de la energía cinética con la cual partió en la parte baja del ascenso se transforma en energía calórica. Debido a la energía potencial que posee y a la construcción de la montaña rusa, el carro inicia un segundo descenso donde recorre 54 m, transformando en energía calorífica el
de la energía cinética con la cual partió en la parte baja del ascenso se transforma en energía calórica. Debido a la energía potencial que posee y a la construcción de la montaña rusa, el carro inicia un segundo descenso donde recorre 54 m, transformando en energía calorífica el ![]() de la energía potencial cuando llega el carro a la parte más baja de la montaña rusa. Debido a la energía cinética que aún posee el carro, inicia un segundo trazado horizontal de 30 m, donde, debido al rozamiento, el
de la energía potencial cuando llega el carro a la parte más baja de la montaña rusa. Debido a la energía cinética que aún posee el carro, inicia un segundo trazado horizontal de 30 m, donde, debido al rozamiento, el ![]() de la energía cinética con la que inició su segundo trazado horizontal se transforma en energía calórica y debido a la energía cinética que aún posee el carro, el carro inicia un segundo ascenso de 45 m donde el
de la energía cinética con la que inició su segundo trazado horizontal se transforma en energía calórica y debido a la energía cinética que aún posee el carro, el carro inicia un segundo ascenso de 45 m donde el ![]() de la energía cinética se transforma en calor, llegando a la parte más alta de la tercera joroba. El carro comienza un tercer descenso de 37 m debido a su energía potencial durante el que transforma en calor el
de la energía cinética se transforma en calor, llegando a la parte más alta de la tercera joroba. El carro comienza un tercer descenso de 37 m debido a su energía potencial durante el que transforma en calor el ![]() al llegar a la parte más baja de la montaña rusa, donde hace su último recorrido horizontal de 50 m hasta detenerse.
al llegar a la parte más baja de la montaña rusa, donde hace su último recorrido horizontal de 50 m hasta detenerse.
Teniendo en cuenta la situación planteada efectúa:
1. El grafico s-t correspondiente.
2. Las diferentes transformaciones de energía que se producen.
3. La desaceleración del carro en el último trayecto horizontal.
4. La altura de las jorobas de la montaña rusa.
5. La velocidad del carro al inicio y al final de los tres recorridos horizontales.
Un capacitor de placas paralelas se carga conectándolo a una batería y luego se desconecta de esta. Si se duplica la distancia de separación entre las placas: ¿cómo cambian el campo eléctrico, la diferencia de potencial y la energía total? Razona tus respuestas.
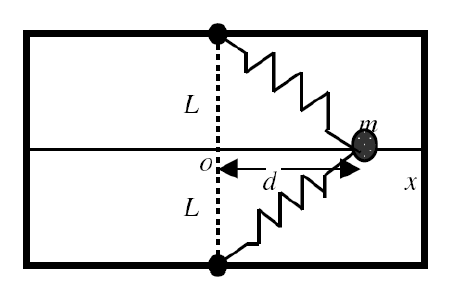
Una partícula de masa m=0.2 kg se une entre dos resortes idénticos, de longitud L=1.2 m, sobre la parte superior de una mesa horizontal sin fricción. Los dos resortes tienen la misma constante elástica ![]() y cada uno está inicialmente en su posición de equilibrio. Si la partícula se separa una distancia d=0.5 m hacia la derecha y después se suelta, como indica la figura, ¿cuál es la velocidad cuando pasa por el punto O (posición de equilibrio)?
y cada uno está inicialmente en su posición de equilibrio. Si la partícula se separa una distancia d=0.5 m hacia la derecha y después se suelta, como indica la figura, ¿cuál es la velocidad cuando pasa por el punto O (posición de equilibrio)?
 Ejercicios FyQ
Ejercicios FyQ