Un bloque de 2.0 kg inicialmente a 0.8 m de altura, comprime inicialmente 10 cm a un resorte de constante k = 600 N/m hasta que sale liberado del mismo. En la parte más baja ingresa a una región donde existe una fuerza de rozamiento de módulo variable, como se ve en la gráfica de la figura.

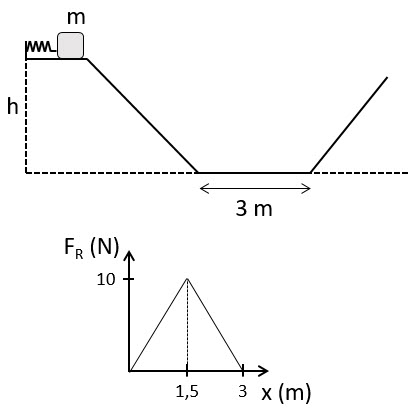
a) En función de los datos anteriores, calcula la máxima altura que alcanzará la masa.

b) ¿Volverá a atravesar toda la zona con rozamiento? Justifica tu respuesta.

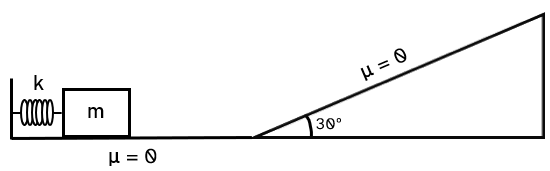
Junto al resorte de la figura, de constante elástica 20 000 N/m, se coloca un cuerpo de 2.5 kg. Se comprime el resorte 7 cm y se suelta el cuerpo. Si el coeficiente de rozamiento es cero, calcula:

a) La rapidez del cuerpo en el plano horizontal.

b) La rapidez que tiene el cuerpo cuando asciende 3 m en el plano inclinado.

c) La distancia que recorre el cuerpo en el plano inclinado hasta detenerse.

Un bloque de masa de 3 kg parte del reposo y se desliza a una distancia de 3 m por la superficie de un plano inclinado un ángulo de . El bloque choca con un resorte de constante de elasticidad 93 N/m al llegar al final del plano. Si el coeficiente de rozamiento es de 0.2, determina:

a) La velocidad con la que llega el bloque al resorte.

b) ¿Cuál es la comprensión máxima del resorte?

c) ¿Hasta qué distancia subirá el bloque después del rebote?

Desde la parte superior de un edificio en llamas, de 15 m de altura, se lanza una persona a una colchoneta de espuma colocada por los bomberos al pie del edificio. Si la colchoneta se hunde 35 cm después de que la persona cae sobre ella:

a) ¿Con qué velocidad toca la persona la colchoneta?

b) ¿Qué aceleración experimenta la persona mientras está en contacto con la colchoneta?

c) ¿Cuánto tiempo dura toda la travesía de la persona?

Una bala de 15 g de masa, que lleva una velocidad de 350 m/s, es disparada contra una masa M = 1.0 kg, inicialmente en reposo, suspendida de una cuerda de 2 m de longitud. La bala penetra en la masa y sale de ella (después de un intervalo de tiempo muy pequeño) con una velocidad de 100 m/s.

a) Calcula el impulso que recibió la masa M.

b) ¿Cuál es la tensión de la cuerda, justo después de ser atravesada M?

c) ¿Cuál es la altura máxima que subirá la masa M?

A un bloque se le da una velocidad de hacia arriba sobre un plano inclinado con un coeficiente de rozamiento de :

a) Determina la altura máxima que alcanza el bloque sobre el plano.

b) Calcula la velocidad con la que regresa el bloque al punto inicial.

Calcula el trabajo y la potencia de una fuerza de 10 dinas que mueve un objeto 25 centímetros, durante 20 segundos, cuando es aplicada con un ángulo de .

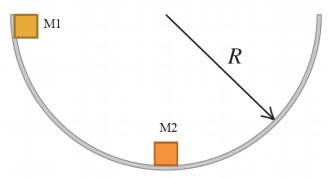
Dos bloques se sueltan del reposo en un tazón hemisférico liso de radio R = 5 m, desde las posiciones que se muestran en la figura. Se puede despreciar a fricción entre las masas y la superficie del tazón. Si la colisión es elástica y , ¿a qué altura sobre el fondo del tazón alcanzarán los bloques después de chocar la primera vez?

Una pelota de softball de 0.220 kg de masa, que se mueve con una rapidez de 8.5 m/s, choca frontal y elásticamente con otra bola que está en reposo. Después de eso, la bola que llega rebota hacia atrás con una rapidez de 3.7 m/s. Calcula:

a) La velocidad de la bola inicialmente en reposo después de la colisión.

b) La masa de la bola inicialmente en reposo.

Un crucero de 270 toneladas parte desde la ciudad de Cartagena hacia la isla de San Andrés a una velocidad de 42.0 m/s y en la mitad del camino observa un barco mercante clase Panamax de 487 toneladas acercándose por la derecha a una velocidad de 38.0 m/s, colisionando perpendicularmente de tal manera que ambos barcos quedan unidos. Determina:

a) La dirección con respecto a la horizontal de la velocidad de los barcos después de la colisión.

b) El módulo de la velocidad de los barcos después de la colisión.

c) Representa en un mismo plano cartesiano a escala las velocidades de las dos embarcaciones antes y después del choque, asumiendo que el punto de la colisión es el origen del plano, es decir, el punto (0, 0).