El mapa de un tesoro da las siguientes pistas: 100 m () , 50 m () y 80 m () . ¿Qué distancia y qué dirección se debe seguir para hallar el tesoro?

Dos cuerpos A y B situados a 2 km de distancia salen simultáneamente uno en persecución del otro con movimiento acelerado (ambos) siendo la aceleración del mas lento (el cuerpo B) de . Deben encontrarse a 3.025 km de distancia del punto de partida de B. Calcula:

a) Tiempo que tardan en encontrarse.

b) Aceleración de A.

c) Sus velocidades en el momento del encuentro.

Dos cuerpos se lanzan simultáneamente desde un mismo punto: uno verticalmente hacia arriba, y otro formando un ángulo con la horizontal. La velocidad inicial de ambos cuerpos es .

a) Hallar la distancia entre los cuerpos a los 1.7 s.

b) Hallar la distancia entre ellos en el momento en el que los vectores de sus velocidades sean mutuamente perpendiculares.

Una partícula se mueve a lo largo del eje OX de un sistema de coordenadas con aceleración constante. En el instante inicial pasa por la posición con una velocidad y en t = 3 s su posición es . Determina:

a) La ecuación de la posición de la partícula en función del tiempo.

b) El espacio recorrido por la partícula entre t = 3 s y t = 6 s.

c) La velocidad media entre t = 4 s y t = 7 s.

d) Los intervalos de tiempo en que la partícula se aleja del origen.

Un móvil se desplaza en el eje X con una velocidad constante. En el instante está en la posición y en el instante está en . ¿Cuál fue su posición, expresada en m, en el instante t = 1 s?

Las ecuaciones del movimiento de dos móviles son:

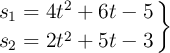
¿Qué relación existe entre los espacios recorridos por ambos móviles al cabo de 5 s? ¿Y entre sus velocidades?

La ecuación de un movimiento es (SI). ¿Cuál es la ecuación de la celeridad? ¿Y la de la aceleración? ¿Qué podemos deducir de ésta última?

Desde lo más alto de un edificio de 50 m de altura se lanza un cuerpo oblicuamente hacia arriba con una velocidad inicial de en una dirección que forma un ángulo con la horizontal, tal que y . Suponiendo nula la resistencia del aire y que la aceleración de la gravedad es de , determina:

a) El vector de posición del móvil en función del tiempo.

b) En qué punto chocará con el suelo, supuesto horizontal.

c) La velocidad del móvil en función del tiempo.

d) Su velocidad en el instante del choque con el suelo.

e) La altura máxima que alcanzará el móvil en su recorrido.

f) La ecuación de la trayectoria de este movimiento.

La siguiente tabla muestra los valores de velocidad de un móvil en función del tiempo:

a) Interpreta dichos valores y realiza una gráfica v-t.

b) Determina la ecuación de la velocidad en función del tiempo. ¿Qué velocidad llevaría a los 15 s?

c) Halla la ecuación de la posición en función del tiempo y realiza la gráfica s-t.

d) Determina la posición en el instante 10 s si inicialmente se encontraba a 5 m del origen.

¿Cuál es el espacio recorrido por la aguja de los minutos del Big Ben al cabo de 10 minutos?

Considera que la distancia desde el eje hasta el extremo de la aguja de los minutos es 3.44 m.