Dos partículas se mueven perpendiculamente una a la otra y con una velocidad de 6 m/s. La masa de una de las partículas es el doble que la otra. Si suponemos el choque entre ambas perfectamente inelástico, ¿cuáles son la velocidad y celeridad después del choque? ¿Qué dirección tiene?

Un patinador de 30 kg lleva una velocidad de cuando choca contra otro patinador que está inmóvil. Después del choque se mueven juntos en la misma dirección y sentido que el primer patinador con una velocidad común de . Calcula la masa del segundo patinador.

Una bala de 8 g se dispara horizontalmente sobre un bloque de madera de 9 kg. Sabiendo que la velocidad del bloque y la bala después del choque es de 4 cm/s. Calcula la velocidad inicial de la bala.

Una silla desliza libremente sobre un piso horizontal pulido con una velocidad inicial de . Si se detiene después de recorrer 2 m, ¿cuál es el coeficiente de fricción entre el piso y la silla?

Una caja de 800 N de peso se encuentra situada en una rampa que forma un ángulo de con la horizontal. Basta con ejercer una fuerza de 200 N paralela a la superficie de la rampa para impedir que la caja se deslice hacia abajo por efecto de su peso.

a) ¿Cuál es el coeficiente de rozamiento estático entre la caja y la rampa?

b) Si el coeficiente de rozamiento dinámico es , ¿con qué fuerza, paralelamente a la superficie de la rampa, es preciso tirar de la caja para que suba con velocidad constante?

Un sistema de tres masas como el que se muestra en la figura se utiliza como dispositivo para determinar el coeficiente de fricción cinético entre la masa y la superficie horizontal:

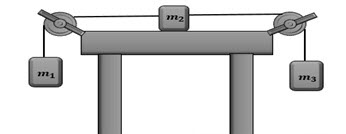
a) Determina el valor del coeficiente de fricción cinético entre la superficie horizontal y la masa , teniendo en cuenta que los valores de las masas , y son de 2.00 kg, 3.40 kg y 8.00 kg respectivamente y la aceleración del sistema es de .

b) Determina el valor de las tensiones de las dos cuerdas.

NOTA: En todos los cálculos se asume que no hay fricción en las poleas y que la cuerda es inextensible.

Un cuerpo de masa 12 kg está sobre una superficie horizontal y sobre él se aplican dos fuerzas; una de 16 N en dirección horizontal y hacia la derecha y la otra de 40 N, formando un ángulo de 37º con la horizontal en el mismo sentido. Calcula el coeficiente de rozamiento cinético si el sistema se mueve con velocidad constante.

En la figura de este problema se representan dos bloques de masas y , unidos entre sí por un hilo liviano que inicialmente estaban en reposo.

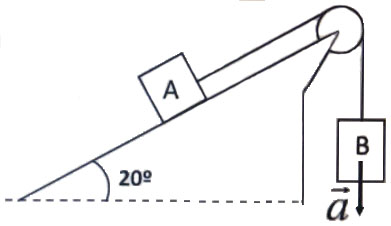
Determina el coeficiente de rozamiento cinético entre las superficies del bloque A y el plano, sabiendo que el bloque B desciende con una aceleración constante de valor .

Un bloque de 200 g desciende con velocidad constante cuando el ángulo de inclinación de un plano es de .

a) Calcula el coeficiente de rozamiento cinético entre el bloque y la superficie del plano.

b) Si se eleva el ángulo hasta los , ¿con qué aceleración descendería el bloque?

Un cuerpo cuyo peso es de 96 N está sobre una superficie horizontal y sobre él se aplican dos fuerzas; una de 18 N en dirección horizontal y hacia la izquierda y la otra de 60 N con un ángulo de con la horizontal en sentido contrario. Calcula el coeficiente de rozamiento estático del sistema si el éste se encuentra en el momento exacto antes de comenzar a moverse.