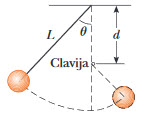
Un péndulo, que consta de una cuerda ligera de longitud L y una esfera pequeña, se balancean en el plano vertical. La cuerda golpea una clavija ubicada a una distancia d bajo el punto de suspensión, como se puede ver en la figura. Demuestra que si el péndulo se libera desde la posición horizontal () y se balancea en un círculo completo con centro de la clavija, el valor mínimo de d debe ser 3L/5.

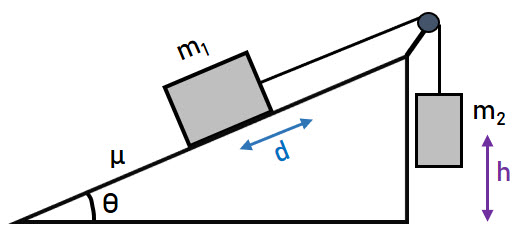
Las masas y se encuentran unidad por una cuerda ligera inextensible que pasa por una polea ideal como se muestra en la figura. El coeficiente de fricción cinético entre la masa y el plano inclinado es . Determina la velocidad de cuando ha avanzado una distancia d hacia arriba, teniendo en cuenta que h > d.

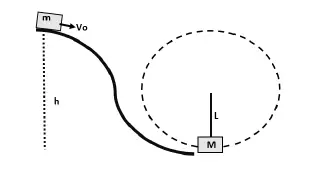
Una partícula de masa m se lanza con una velocidad inicial desde una altura h. Si en el trayecto AB se degrada una cantidad de energía igual a y si m choca de forma perfectamente inelástica con M, determina la mínima de m para que las partículas describan un movimiento circular.

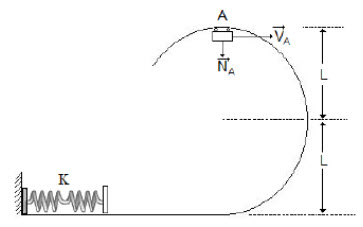
Un carro de montaña rusa de masa m (kg) se mueve sobre un riel sin fricción por la vía que se muestra en la figura. Al pasar por el punto A, la fuerza normal que ejerce la vía sobre el carro es . Cerca de A la vía es circular y de radio L (m). Cuando el carro llega a la parte inferior de la vía lo detiene un amortiguador de resorte con constante de restitución, k (N/m). Calcula la máxima deformación del resorte.

¿Cuál es la máxima altura desde la que puede saltar una persona de 70 kg, si al llegar al suelo mantiene las piernas rígidas, suponiendo que los huesos de las piernas tienen 0.5 m de longitud y pueden soportar como máximo una deformación unitaria de ? Supón que la superficie del hueso en promedio es de y que el módulo de Young de los huesos es . Debes considerar que las articulaciones son infinitamente resistentes de forma que no absorben energía potencial.

Determina el trabajo realizado por la fuerza a lo largo de las curva para t que pertenece a [0, 2].

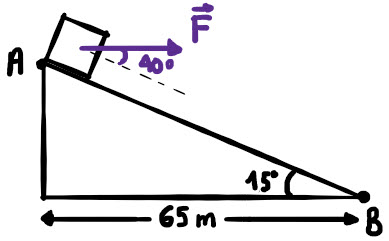
Un bloque de 75 kg es arrastrado desde el punto A hasta el punto B del plano inclinado por una fuerza F con una aceleración de . Si la superficie es rugosa y tiene un coeficiente de rozamiento de 0.68, calcula:

a) El trabajo realizado por la fuerza F.

b) El trabajo realizado por la normal.

c) El trabajo realizado por el peso.

d) El trabajo realizado por la fuerza de rozamiento.

Un cilindro macizo y homogéneo de 6 kg rueda sin rozamiento por un plano inclinado de a lo largo de 10 m. Si parte del reposo, halla al final del plano:

a) La velocidad lineal.

b) La energía cinética de rotación.