Ejercicios FyQ
Dos puntos materiales A y B de masas iguales están situados en el plano XY. El punto A viene determinado por un vector de posición cuyo módulo vale 2 y forma un ángulo de 
con el eje X, mientras que el punto B se puede encontrar en cualquier punto del eje Y. ¿Dónde estará situado el centro de masas?
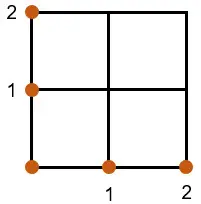
El centro de masas de un sistema formado por cinco masas puntuales iguales colocadas en la forma que indica la figura está en la bisectriz del ángulo. ¿A qué distancia del vértice se encuentra?
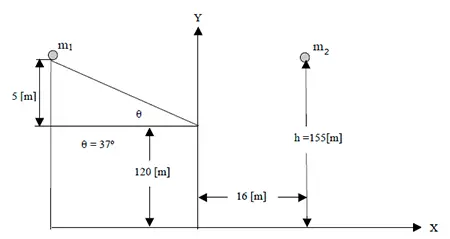
Las partículas 
y 
tienen movimientos independientes. La partícula 1 se deja libre sobre el plano liso, inclinado un ángulo 
, mientras que la partícula 2 se lanza verticalmente hacia abajo desde la altura h con una velocidad inicial de 
. La partícula 2 inicia su movimiento en el instante en que la partícula 1 abandona el plano inclinado. Determina, para t = 2 s después de que la partícula 1 abandona el plano inclinado:
a) La posición del centro de masas del sistema constituido por 
y 
.
b) La velocidad del centro de masas.
c) El momento angular de cada partícula respecto al origen del sistema de referencia.
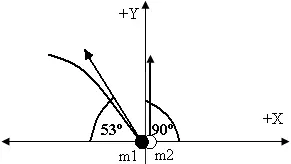
La figura muestra un sistema formado por dos partículas con masas 
y 
. Las partículas se lanzan simultáneamente y sus velocidades iniciales son 
y 
. Para el instante t = 2 s, determina:
a) La posición del centro de masas del sistema respecto al origen.
b) La velocidad del centro de masas del sistema respecto al origen.
c) El momento angular del sistema respecto al origen.
d) El momento lineal de la partícula 1 respecto al centro de la masas.
Un sistema de dos partículas de masas 2 y 3 kg se mueven en el plano XY. En un instante dado, las posiciones y velocidades de las partículas son:
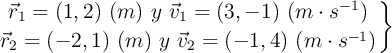
a) Calcula la posición del centro de masas (CM) del sistema.
b) Determina la velocidad del centro de masas.
c) Calcula el momento lineal total del sistema.
d) Determina el momento angular total del sistema respecto al origen.
e) Si las partículas están sometidas a las fuerzas externas 
y 
, calcula la aceleración del centro de masas.
Una rueda de bicicleta se sostiene del eje con una cuerda suspendida del techo tal como muestra la figura.
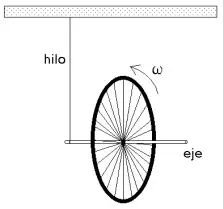
El punto de amarre se ubica a una distancia de 20 cm del centro de la rueda, la llanta pesa 4 Kg y tiene un radio de 30 cm. La rueda se hace girar a 10 rev/s. El eje se orienta inicialmente de manera horizontal.
a) Demuestra que el eje de la rueda se mantendrá en posición horizontal y que esta realizará un movimiento circular.
b) Calcula la velocidad angular.
En la figura que se muestra, determina la tension en el cable, si la barra es homogénea y de masa insignificante.
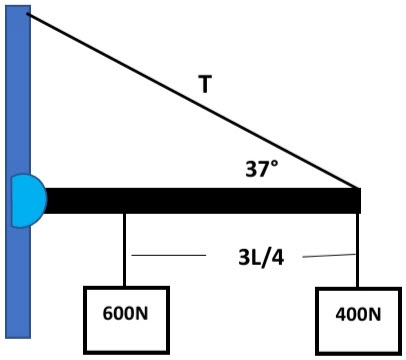
En la siguiente figura, la viga uniforme de 725 N de peso está sujeta a un pasador en el punto A:
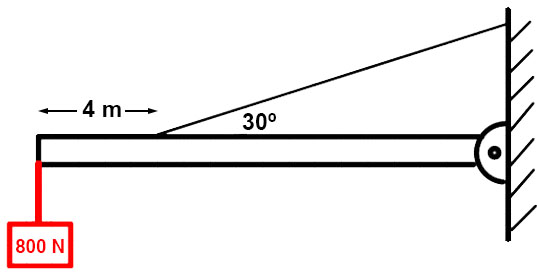
a) Determina la tensión en la cuerda.
b) Calcula las componentes de la fuerza que ejerce el apoyo sobre la viga.
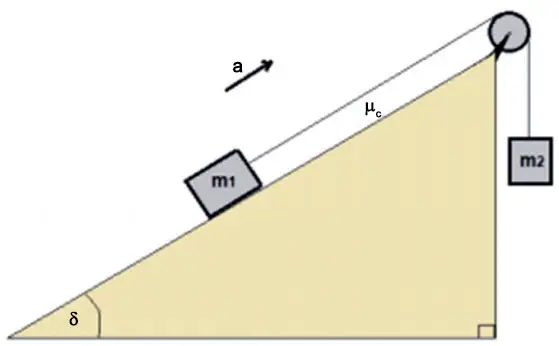
Se observan en la figura dos bloques, de masas 
y 
, que se encuentran unidos por una cuerda ideal (sin masa e inextensible) a través de una polea sin fricción de radio R y momento de inercia I. La superficie tiene un coeficiente de roce cinético 
. Los bloques se mueven con una aceleración a.
a) Representa en un esquema las fuerzas que intervienen sobre los objetos del sistema.
b) Determina las expresiones para calcular las tensiones en la cuerda, en función de los datos dados.
c) Calcula las tensiones con los datos: 
; 
; 
; 
; 
.
Un elevador puede acelerar a 
y después desacelerar a 
. Determina el tiempo más corto que tardaría en llegar a un piso de una altura de 40 ft, sabiendo que ha de detenerse al llegar.