Ejercicios FyQ
El columpio gigante de una feria local consiste en un eje vertical con varios brazos horizontales unidos a su extremo superior, como puedes ver en la figura adjunta. Cada brazo sostiene un asiento suspendido de un cable de 5.00 m, sujeto al brazo en un punto a 3.00 m del eje central.
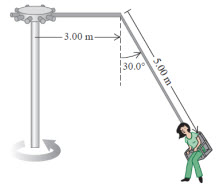
a) Calcula el tiempo de una revolución del columpio si el cable forma un ángulo de 
con la vertical.
b) El ángulo depende del peso del pasajero para una velocidad de giro determinada?
Un mortero dispara un proyectil con una velocidad inicial 
formando un ángulo 
con la horizontal. A 20.0 m de él un tanque parte del reposo en línea recta con una aceleración constante de 
. Determina la velocidad mínima inicial del proyectil para que pueda impactar en el tanque.
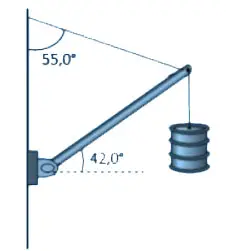
Una barra ingrávida esta suspendida sobre un pivote tal como muestra la figura. Si el cilindro que suspende en el extremo de la barra tiene un peso de 600 N:
a) Dibuja el diagrama del cuerpo libre de la barra.
b) Escribe las ecuaciones de las condición de equilibrio.
c) Calcula la magnitud de tensión oblicua.
La densidad relativa del agua en la superficie del océano es de 1.025. Calcula:
a) La densidad del agua en el fondo, donde la presión es de 500 atmósferas.
b) El peso de un metro cúbico de agua a esa profundidad.
Datos: módulo de elasticidad del agua: 
, densidad del agua pura: 
.
Si se sabe que la cantidad de oxígeno a cualquier altitud es 
, ¿cuánto será la presión de oxígeno a 500 metros de altitud?
Una varilla de aluminio soporta una tensión longitudinal de 
y la deformación longitudinal es de 
. Si la varilla tiene 85 cm de longitud inicial y el modulo de Young para este material es de 
, determina lo siguiente:
a) La longitud final de la varilla.
b) La magnitud de la fuerza aplicada que deformó la varilla si su sección transversal es 
.
c) ¿De qué diámetro será la varilla?
Una barra metálica delgada y uniforme, de 2.00 m de longitud y con un peso de 90.0 N, cuelga verticalmente del techo en un pivote sin fricción colocado en el extremo superior. De repente, una pelota de 3.00 kg, que viaja inicialmente a 10.0 m/s en dirección horizontal, golpea la barra 1.50 m abajo del techo. La pelota rebota en dirección opuesta con rapidez de 6.00 m/s. Calcula la rapidez angular de la barra inmediatamente después del choque.
Dos bloques cuyas masas son 
y 
están conectados por una cuerda ligera que pasa sobre una polea sin fricción, como se muestra en la figura.
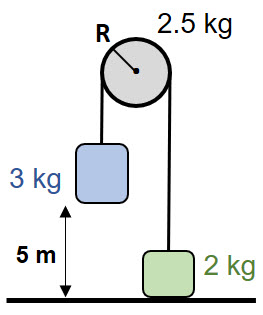
La polea tiene un radio R = 20.0 cm y masa M = 2.50 kg. Si el sistema se libera desde el reposo determina, usando consideraciones energéticas:
a) La rapidez de los bloques cuando el bloque 1 desciende una distancia de 5.00 m.
b) La magnitud de la aceleración de los bloques.
Una esfera de radio r = 24.5 cm y masa m = 1.20 kg parte del reposo y rueda hacia abajo sin deslizamiento sobre una rampa con 
de inclinación que tiene 10.0 m de largo. Calcula las velocidades de traslación y rotación cuando llega a la parte inferior de la rampa.
El momento de inercia de una esfera sólida con respecto a un eje de rotación que pasa por su centro de masa es 
.
Una mosca tiene el vector de posición 
. Calcula:
a) El vector velocidad instantánea y el vector aceleración instantánea para t = 5 s.
b) Los módulos de la aceleración tangencial y normal para t = 2 s.
c) El radio de curvatura para t = 2 s y la ecuación de la trayectoria.