P.-S.
a) La función de onda inicial estará normalizada cuando cumpla la condición:
![\color[RGB]{2,112,20}{\bm{\int_{0}^{L} |\Psi(x, 0)|^2\ dx = 1}} \color[RGB]{2,112,20}{\bm{\int_{0}^{L} |\Psi(x, 0)|^2\ dx = 1}}](local/cache-vignettes/L212xH54/74d83981dcbb5ac46342991fae33c0e3-b7515.png?1748518547)
Escribes la ecuación sustiyendo la función de onda:
![\int_{0}^{L} \left( \sqrt{\frac{30}{L^5}} \, x (L - x) \right)^2 dx = \color[RGB]{2,112,20}{\bm{\frac{30}{L^5} \int_{0}^{L} x^2 (L - x)^2\ dx}} \int_{0}^{L} \left( \sqrt{\frac{30}{L^5}} \, x (L - x) \right)^2 dx = \color[RGB]{2,112,20}{\bm{\frac{30}{L^5} \int_{0}^{L} x^2 (L - x)^2\ dx}}](local/cache-vignettes/L484xH69/d380354b0642b7832863c214b2e394ba-88dd8.png?1748518547)
Si desarrollas el cuadrado y divides en tres integrales:
![\frac{30}{L^5} \left[ L^2 \int_{0}^{L} x^2 \, dx - 2L \int_{0}^{L} x^3 \, dx + \int_{0}^{L} x^4 \, dx \right] = 1 \frac{30}{L^5} \left[ L^2 \int_{0}^{L} x^2 \, dx - 2L \int_{0}^{L} x^3 \, dx + \int_{0}^{L} x^4 \, dx \right] = 1](local/cache-vignettes/L447xH54/052bace1481ebdfd7b966aa53d779630-32e66.png?1748518547)
Las integrales son inmediatas y las calculas entre los límites de integración:
![\frac{30}{L^5} \left( L^2\cdot \frac{L^3}{3} - 2L\cdot \frac{L^4}{4} + \frac{L^5}{5} \right) = \color[RGB]{0,112,192}{\bm{\frac{30}{L^5} \left( \frac{L^5}{3} - \frac{L^5}{2} + \frac{L^5}{5} \right)}} \frac{30}{L^5} \left( L^2\cdot \frac{L^3}{3} - 2L\cdot \frac{L^4}{4} + \frac{L^5}{5} \right) = \color[RGB]{0,112,192}{\bm{\frac{30}{L^5} \left( \frac{L^5}{3} - \frac{L^5}{2} + \frac{L^5}{5} \right)}}](local/cache-vignettes/L512xH55/9fbd1e95e7c488b711dee201f9aa0601-9f8f7.png?1748518548)
Si sacas factor común  y simplificas:
y simplificas:
![\frac{30\cdot \cancel{L^5}}{\cancel{L^5}} \left( \frac{1}{3} - \frac{1}{2} + \frac{1}{5} \right) = 30 \left( \frac{10}{30} - \frac{15}{30} + \frac{6}{30} \right) = \fbox{\color[RGB]{192,0,0}{\bm{30 \left( \frac{1}{30} \right) = 1}}} \frac{30\cdot \cancel{L^5}}{\cancel{L^5}} \left( \frac{1}{3} - \frac{1}{2} + \frac{1}{5} \right) = 30 \left( \frac{10}{30} - \frac{15}{30} + \frac{6}{30} \right) = \fbox{\color[RGB]{192,0,0}{\bm{30 \left( \frac{1}{30} \right) = 1}}}](local/cache-vignettes/L562xH54/8237f800da8c3f9fd5b1f393f9101993-d7799.png?1748518548)
Como puedes ver, la función de onda está normalizada.
b) La ecuación de los estados estacionarios de un pozo infinito es:
![\color[RGB]{2,112,20}{\bm{\psi_n(x) = \sqrt{\frac{2}{L}}\cdot sen \left( \frac{n \pi x}{L} \right) }} \color[RGB]{2,112,20}{\bm{\psi_n(x) = \sqrt{\frac{2}{L}}\cdot sen \left( \frac{n \pi x}{L} \right) }}](local/cache-vignettes/L271xH56/6603ae6c6e1bbe7601218ca4e625ebff-778d3.png?1748518548)
Tienes que expresar la función de onda como combinación lineal de los estados estacionarios:
![\color[RGB]{0,112,192}{\bm{\Psi(x, 0) = \sum_{n=1}^{\infty} c_n\cdot \psi_n(x)}} \color[RGB]{0,112,192}{\bm{\Psi(x, 0) = \sum_{n=1}^{\infty} c_n\cdot \psi_n(x)}}](local/cache-vignettes/L241xH60/62bfdf01cdba5772ee24b568fd94c83a-76586.png?1748518548)
Los coeficientes
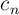
los calculas de esta manera:

Si operas con las constantes que está fuera del integrando tienes:

La resolución de la integral la haces en dos partes:

Combinas los términos anteriores y tienes:

Si tienes en cuenta que para valores pares de «n» los términos se cancelan y simplificas, obtienes:
![\color[RGB]{0,112,192}{\bm{c_n = \frac{4 \sqrt{15}}{n^3 \pi^3} \left( 1 - (-1)^n \right)}} \color[RGB]{0,112,192}{\bm{c_n = \frac{4 \sqrt{15}}{n^3 \pi^3} \left( 1 - (-1)^n \right)}}](local/cache-vignettes/L237xH53/e6d8d177177f3de76378443068737276-a0076.png?1748518548)
Por lo tanto, para valores pares de «n» los coeficientes son nulos y para valores impares de «n» obtienes:
![\fbox{\color[RGB]{192,0,0}{\bm{c_n = \frac{8 \sqrt{15}}{n^3 \pi^3}}}} \fbox{\color[RGB]{192,0,0}{\bm{c_n = \frac{8 \sqrt{15}}{n^3 \pi^3}}}}](local/cache-vignettes/L112xH44/04c2a1b221d1d61b754b6118114834ff-8bf3a.png?1748518548)
c) La función de onda en función del tiempo, escrita como combinación lineal de los estados estacionarios, es:
![\color[RGB]{192,0,0}{\bm{\Psi(x, t) = \sum_{n=1, 3, 5, \dots} \frac{8\sqrt{15}}{n^3\pi^3} \sqrt{\frac{2}{L}}\cdot sen \left( \frac{n \pi x}{L} \right) e^{\frac{-i E_n t}{\hbar}}}} \color[RGB]{192,0,0}{\bm{\Psi(x, t) = \sum_{n=1, 3, 5, \dots} \frac{8\sqrt{15}}{n^3\pi^3} \sqrt{\frac{2}{L}}\cdot sen \left( \frac{n \pi x}{L} \right) e^{\frac{-i E_n t}{\hbar}}}}](local/cache-vignettes/L492xH64/03b030ad0729d2fb05ce484362f06f3e-51349.png?1748518548)
donde el término
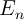
es:
![\color[RGB]{2,112,20}{\bm{E_n = \frac{n^2 \pi^2 \hbar^2}{2mL^2}}} \color[RGB]{2,112,20}{\bm{E_n = \frac{n^2 \pi^2 \hbar^2}{2mL^2}}}](local/cache-vignettes/L133xH51/f2f52bd80229fffb3461b7c22699af1c-00c5a.png?1748518548)
d) Como
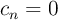
para cualquier valor par de «n», la probabilidad de encontrar
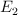
es nula, es decir:
![\fbox{\color[RGB]{192,0,0}{\bm{P(E_2) = |c_2|^2 = 0}}} \fbox{\color[RGB]{192,0,0}{\bm{P(E_2) = |c_2|^2 = 0}}}](local/cache-vignettes/L196xH35/647b31c714d943188eaf53f7bde46f47-4c1ee.png?1748518548)
Esto ocurre porque la función de onda es una combinación de estados estacionarios impares, como has calculado en el segundo apartado del problema.
![]() . En el instante t = 0, la función de onda de la partícula viene dada por:
. En el instante t = 0, la función de onda de la partícula viene dada por:
![]() como una combinación lineal de los estados estacionarios
como una combinación lineal de los estados estacionarios ![]() del pozo infinito.
del pozo infinito.![]() en un tiempo t > 0.
en un tiempo t > 0. Ejercicios FyQ
Ejercicios FyQ