Número atómico y masa atómica
|
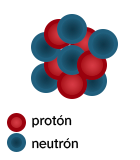
Ya sabes que los protones y los neutrones son las partículas que componen el núcleo de los átomos, por eso ambos se conocen como «nucleones». Hay dos magnitudes que tienen mucha importancia en los átomos y debes saber interpretar qué es cada una de ellas. Número atómico (Z). Es el número de protones que hay en el núcleo de un átomo. Es lo que caracteriza a cada elemento, es decir, todos los átomos que tienen el mismo número de protones son átomos del mismo elemento químico. En la imagen, Z = 5 y se trataría de un átomo de boro (B). Número másico o masa atómica (A). Se corresponde con el número de nucleones que hay en el núcleo, es decir, con la suma de los protones y neutrones que forman el núcleo. En a imagen, A = 11 porque coincide con el número de nucleones representados. |
|
| Si echas un vistazo a la tabla periódica podrás ver que la masa atómica de los elementos es un dato que contiene decimales y, en muchos casos, con valores decimales que no son despreciables. Si la masa atómica es la suma de protones y neutrones de un núcleo, ¿cómo es posible que aparezcan valores decimales? |  |
Los isótopos son la respuesta
Puedes entender la aparente contradicción entre los valores decimales de la masa atómica y su definición como número de nucleones en el núcleo, si prestas atención a un detalle que quizás hayas pasado por alto. Hasta ahora has podido leer que los elementos se caracterizan por su número atómico y que los átomos que tienen el mismo número de protones son átomos del mismo elemento... ¿Quiere eso decir que átomo y elemento no es lo mismo?
Hay 118 elementos, por ahora
Los elementos son los que están recogidos en la tabla periódica y, a día de hoy, son 118. Están ordenados en orden creciente de su número atómico, de izquierda a derecha.
.png)
Esto no quiere decir que solo existan 118 tipos de átomos, sino que todos los tipos de átomos que se conocen se pueden clasificar como estos elementos. Entonces, ¿cuál es la diferencia entre ellos?
Si los átomos de un mismo elemento tienen el mismo número atómico (mismo número de protones), el quid de la cuestión está en qué pasa con sus neutrones, que son los otros nucleones a tener en cuenta.
Un ejemplo te ayudará a entenderlo
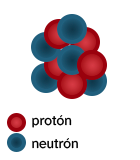
Vamos a volver a nuestro ejemplo inicial, el boro. Fíjate en las dos imágenes:
|

|
Si cuentas, verás que las dos tienen el mismo número de esferas rojas (protones) y por eso ambos átomos son de boro. Sin embargo, la diferencia entre ellos está en el número de esferas azules (neutrones). La primera imagen contiene cinco neutrones, mientras que la segunda imagen contiene seis neutrones. Se dice que ambos átomos son isótopos.
Estos dos núcleos corresponden a los dos isótopos del boro que son estables. Existen otros 14 isótopos más, pero son inestables y son muy poco frecuentes. Son llamados 10B (o B-10) y 11B (o B-11).
No todos los isótopos son igual de frecuentes
Al analizar los átomos de boro que hay en la naturaleza se encuentra que los más frecuentes son los que has visto, aunque no están en la misma proporción. Llamamos abundancia relativa al porcentaje de cada isótopo que se encuentra en la naturaleza. Los datos de masa y abundancia relativa de los isótopos estables del boro son:
- 10B: 10.013 u y 19.9 %
- 11B: 11.009 u y 80.1 %
Para determinar la masa atómica del elemento boro, debes hacer la media ponderada de las masas de sus isótopos estables:
\[\color{darkgreen}{A_B = \frac{m_{^{10}B}\cdot \%_{^{10}B} + m_{^{11}B}\cdot \%_{^{11}B}}{100}} = \frac{10.013\cdot 19.9 + 11.009\cdot 80.1}{100} = \color{darkred}{\boxed{10.811\ u}}\]
Si comparas el valor obtenido, y redondeado a cinco cifras significativas, con el valor de tu tabla periódica, podrás ver que es el mismo.
Son átomos de un mismo elemento que tienen distinto número de neutrones.