Saltar la navegación

2. Orígenes de la teoría cuántica

Radiación electromagnética

Ondas electromagnéticas

Para entender los fenómenos que vas a estudiar es necesario hacer un repaso sobre la radiación electromagnética. Esta radiación se propaga en forma de ondas:

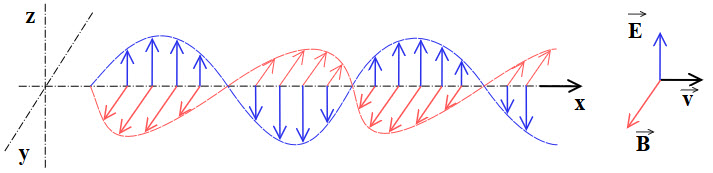
Onda_electromagnética
Wikimedia Commons - SuperManu. Onda electromagnética (CC BY-SA)

Recuerda que una onda electromagnética es aquella que se puede propagar en el vacío, en ausencia de medio material alguno, y cuya dirección de propagación es perpendicular a la oscilación de los campos magnético y eléctrico. A este tipo de ondas se les llama también ondas transversales.

Ondas en las que la vibración es perpendicular a la velocidad de propagación.

La radiación electromagnética se caracteriza, como todas las ondas, por su frecuencia o por su longitud de onda. Ambas magnitudes están relacionadas con la velocidad de propagación por la expresión:

\[\color[RGB]{2,112,20}{\bf{v = \lambda\cdot \nu}}\]

En el caso de que la radiación viaje en el vacío, la velocidad de propagación sería la velocidad de la luz «c».

Explicación en vídeo

A continuación, puedes ver un vídeo en el que explico qué es la radiación electromagnética, cuáles son las magnitudes que usamos para caracterizarla y cómo interpretar el espectro electromagnético. Quizás te pueda servir para refrescar o comprender esta primera parte del tema.

Acción-Educación / EjerciciosFyQ. Radiación electromagnética (Licencia estándar de YouTube)

Ejercicios para practicar

Te presento dos ejercicios resueltos en los que se relacionan la frecuencia y la longitud de onda de una radiación. Te pueden servir de ayuda para terminar de entender cómo trabajar esta parte.

Primer ejercicio:

¿Cuál es la longitud de onda (en nanómetros) de la luz con una frecuencia de 8.6·1013 Hz?

Resolución del  primer ejercicio.

Segundo ejercicio:

¿Cuál es la frecuencia en (Hz) de la luz con una longitud de onda de 566 nm?

Resolución del segundo ejercicio.

Si lo necesitas, descarga en este enlace el archivo EDICO con los ejercicios y las resoluciones.

La longitud de onda y la frecuencia siguen la siguiente relación: \[\color[RGB]{2,112,20}{\bf{c = \lambda\cdot \nu}}\] Despejas: \[\color[RGB]{2,112,20}{\bf{\lambda = \frac{c}{\nu}}}\] Sustituyes y calculas: \[\lambda = \frac{3\cdot 10^8\ \cancel{m}\cdot \cancel{s^{-1}}}{8.6\cdot 10^{13}\ \cancel{s^{-1}}}\cdot \frac{10^9\ nm}{1\ \cancel{m}} = \color[RGB]{192,0,0}{\boxed{\bf{3.5\cdot 10^3\ nm}}}\]

La longitud de onda y la frecuencia siguen la siguiente relación: \[\color[RGB]{2,112,20}{\bf{c = \lambda\cdot \nu}}\] Despejas: \[\color[RGB]{2,112,20}{\bf{\nu = \frac{c}{\lambda}}}\] Sustituyes y calculas: \[\nu = \frac{3\cdot 10^8\ \cancel{m}\cdot s^{-1}}{566\cdot 10^{-9}\ \cancel{m}} = \color[RGB]{192,0,0}{\boxed{\bf{3\cdot 10^{17}\ s^{-1}}}}\]

Espectro electromagnético

El espectro electromagnético que nos llega del Sol abarca un rango de frecuencias y longitudes de onda que permite clasificar a esta radiación por intervalos y por los efectos que provocan sobre la materia y sobre los seres vivos. Aquí puedes ver ilustrado este espectro y los usos que damos a los distintos rangos de frecuencia:

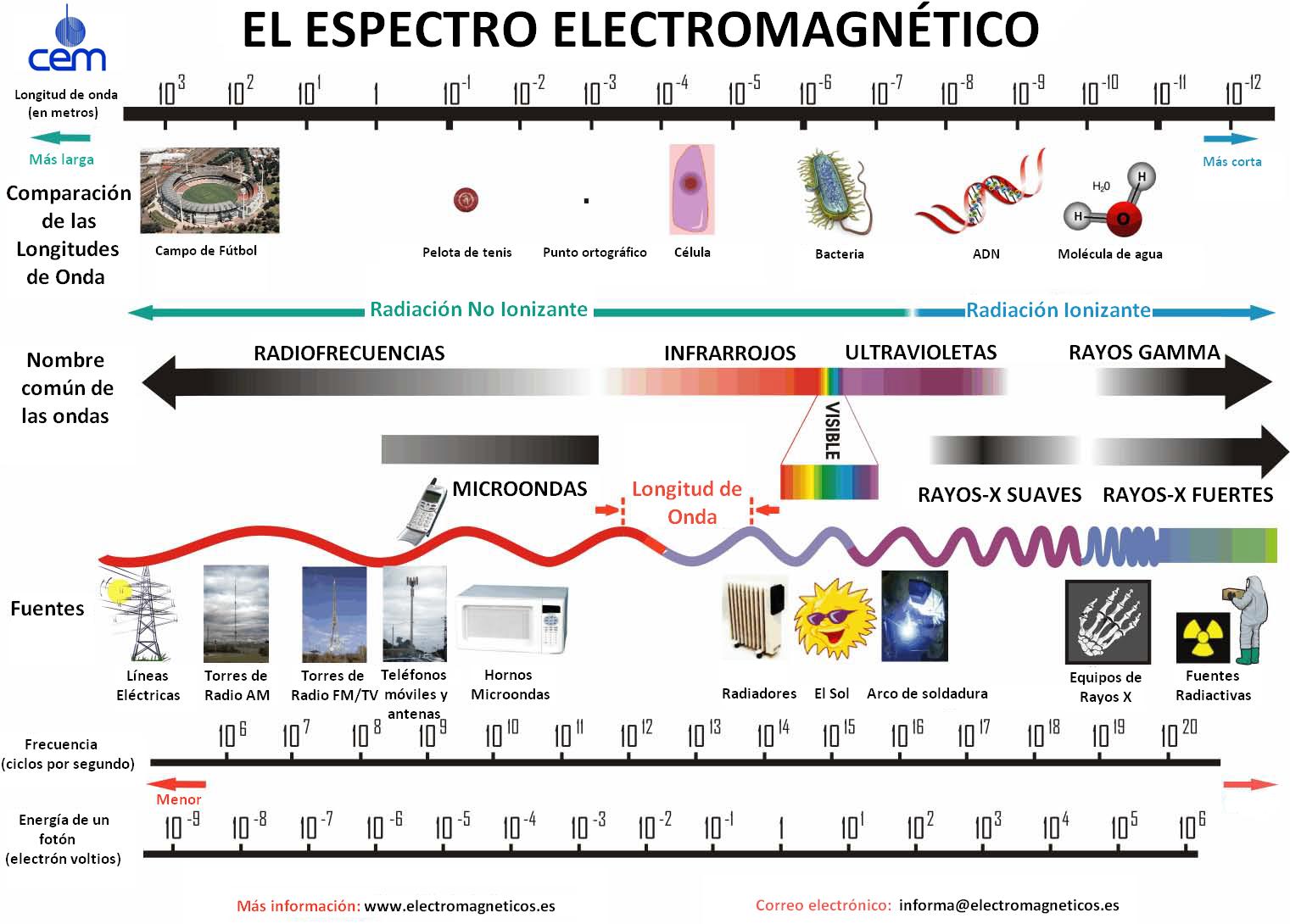
Espectro electromagnético
Electromagnéticos. Espectro electromagnético. (Todos los derechos reservados)

Como puedes ver, cuanto mayor es la frecuencia de la radiación (o menor su longitud de onda), mayor es su energía.

Ejercicio de repaso o refuerzo

Pregunta

¿Cuál es la frecuencia de una onda electromagnética de 750 nm de longitud de onda?

Respuestas

7.5·1011 Hz.

4·1012 Hz.

4·1014 Hz.

7.5·10-7 Hz.

Retroalimentación

Espectros atómicos

A la vez que Rutherford explicaba el resultado de su experimento y creaba su modelo atómico, varios científicos estaban trabajando en el laboratorio con ciertos elementos en los que observaban hechos insólitos como lo que puedes ver en esta imagen:

Espectros de emisión
Curiosoando. Espectros de emisión. (CC BY-SA)

Son las llamas que se generan cuando se queman sales de distintos metales... ¡Y tienen colores distintos!

Lo que ves en la imagen son espectros de emisión. Su estudio cualitativo requiere de sistemas experimentales que permitan su registro y análisis. Es lo que vas a aprender ahora. 

¿Qué son los espectros atómicos?

A finales del siglo XIX se descubrió que si se excitaban muestras de elementos químicos en estado gaseoso, estos eran capaces de interaccionar con la radiación dando lugar a emisiones que seguían una regla bien definida, las llamadas «series espectrales».

Esta interacción entre la radiación y la materia puede ser de dos modos: de emisión o de absorción.

Espectros
m&m. Espectros atómicos (Todos los derechos reservados)
 Espectro de absorción. Se ilumina la muestra con luz blanca, que contiene todas las frecuencias del espectro, y se analiza la luz que atraviesa la muestra.

Espectro de emisión. Se excita la muestra proporcionándole una gran cantidad de energía y se analiza la radiación que emite la muestra cuando se relaja.

Observa que ambos registros son complementarios. Si se superponen se obtiene el espectro de la luz blanca. Esto hace que los espectros atómicos sean una magnífica manera de analizar muestras en las que se busque la presencia de ciertos elementos. Una aplicación podría ser la detección de mercurio en muestras analizadas, en la industria alimentaria o en los cosméticos.

Si haces clic en este enlace puedes echar un vistazo a un trabajo de fin de grado de Ingeniería Química en el que su autora determina la presencia de metales pesados en cosméticos de venta en España, usando la espectroscopía de absorción atómica.

En la web Educaplus tienes una animación en la que puedes ver los espectros de emisión y absorción de los elementos de tabla periódica de los que se conocen.

Trata de responder a estas preguntas y luego comprueba tus respuestas con las que se proponen como solución:

¿En qué se diferencian los espectros de dos elementos químicos distintos?

Los espectros de los elementos químicos son específicos, es decir, que cada elemento químico presenta un espectro de emisión y/o absorción distinto. Esto se debe a que su distribución electrónica es distinta en cada caso y los espectros se obtienen como consecuencia de las transiciones electrónicas en las capas de cada átomo.

¿Cómo han influido las mejoras de los espectroscopios para plantear nuevos modelos de la estructura atómica? Pon ejemplos

Cuando hablamos de espectroscopia nos referimos a cómo interacciona la radiación electromagnética con la materia. Los distintos tipos de interacción tienen que ver con los niveles energéticos en los que se encuentran los electrones dentro de los átomos.

Cuando nos referimos a la estructura atómica debemos tener en cuenta que podemos conocer su estructura externa a partir de técnicas como la absorción y/o emisión de energía por parte de los átomos (series espectrales), los fenómenos de fluorescencia o la interacción con radiación ionizante, como los rayos X.

Cada una de estas técnicas ha proporcionado datos de cómo se excitan o relajan los electrones, es decir, ascienden o descienden de unos niveles de energía a otros.

Los espectros de absorción o emisión permitieron conocer los niveles de energía en los que están situados los electrones externos de cada átomo y así conocer sus configuraciones electrónicas y cómo pueden interaccionar unos átomos con otros. Esto dio lugar al modelo mecano-cuántico del átomo.

Gracias a la fluorescencia se conoce cómo se sitúan los electrones de los átomos que están formando moléculas, con lo que se pudieron corroborar los postulados atómicos y las predicciones de interacción entre átomos, es decir, los modelos de enlace.

Gracias a la espectroscopia de rayos X se ha podido hacer lo mismo que en el caso de la espectroscopia fluorescente, pero aplicado a los compuestos cristalinos.

Series espectrales y ley de Rydberg

Sir Joseph J. Thomson
Wikimedia Commons. Johannes Rydberg. (Dominio público)

Johannes Rydberg (1854-1919) fue un físico experimental sueco, que desarrolló toda su vida profesional en la universidad de Lund. En 1888 dedujo la expresión matemática que permitía predecir la longitud de onda que tendrían las marcas de los espectros atómicos. Es una ley empírica que permitió avanzar en el estudio teórico de la estructura atómica y que Niels Bohr, en 1913, validó teóricamente.

Analizó los espectros obtenidos con muchos elementos distintos y observó que las líneas que aparecían podían ser agrupadas según su número de onda, «k», llegando a deducir una ley empírica que predecía las líneas del espectro del átomo de hidrógeno, primero, y de otros elementos más tarde.

\[\color[RGB]{2,112,20}{\bf{k = \frac{1}{\lambda} = R\left(\frac{1}{n_1^2} - \frac{1}{n_2^2}\right)}}\]

En esta ecuación los valores «n1» y «n2» son números naturales y se cumple siempre que n2 > n1, por lo que el paréntesis es positivo. La constante «R» es la constante de Rydberg y su valor es 1.097·107 m-1.

Dependiendo del valor de «n1» se obtienen distintas series espectrales. Podemos identificar el valor de «n1» como el nivel de menor energía al que llega un electrón cuando se relaja desde otro nivel de mayor energía, «n2». Las series espectrales reciben los siguientes nombres:

  • Serie de Lyman: n1 = 1 y n2 puede ser 2, 3, 4, 5...
  • Serie de Balmer: n1 = 2 y n2 puede ser 3, 4, 5, 6...
  • Serie de Paschen: n1 = 3 y n2 puede ser 4, 5, 6, 7...
  • Serie de Bracket: n1 = 4 y n2 puede ser 5, 6, 7...
  • Serie de Pfund: n1 = 5 y n2 puede ser 6, 7...

Una vez que estudies y comprendas el modelo atómico de Bohr, podrás entender la explicación teórica de estas series.

Dos ejercicios para practicar

Primer ejercicio

En el espectro del átomo de hidrógeno hay una línea a 1.02·10-7 m. Sabiendo que n = 1, ¿cuál es el nivel energético superior?

Dato: R = 1.097·107 m-1.

Lectura facilitada

Partiendo de la ecuación de Rydberg, y teniendo en cuenta el valor de «n1»:

\[\frac{1}{\lambda} = R\left(\frac{1}{n_1^2} - \frac{1}{n_2^2}\right)\ \to\ \color[RGB]{2,112,20}{\bf{\frac{1}{\lambda} = R\left(1 - \frac{1}{n_2^2}\right)}}\]

Debes despejar «n2» como paso previo al cálculo:

\[\frac{1}{\lambda\cdot R} = 1 - \frac{1}{n_2^2}\ \to\ \frac{1}{n_2^2} = 1 - \frac{1}{\lambda\cdot R}\ \to\ \color[RGB]{2,112,20}{\bf{n_2 = \sqrt{\frac{1}{1 - \frac{1}{\lambda\cdot R}}}}}\]

Sustituyes los valores y calculas:

\[n_2 = \sqrt{\frac{1}{1 - \frac{1}{1.02\cdot 10^{-7}\ \cancel{m}\cdot 1.097\cdot 10^7\ \cancel{m^{-1}}}}}\ \to\ \color[RGB]{192,0,0}{\boxed{\bf{n_2 = 3}}}\]

Segundo ejercicio

Determina la frecuencia de la radiación emitida por un átomo de hidrógeno cuando un electrón transita desde la cuarta capa hasta la segunda. ¿A qué serie espectral corresponde esta transición?

Datos: R = 1.097·107 m-1 ; c = 3·108 m·s-1.

Lectura facilitada

A partir de los datos del enunciado, deduces que n1 = 2 y n2 = 4, es decir, el menor nivel de energía es el 2 y eso se corresponde con la serie de Balmer. Puedes calcular el número de onda con la ecuación de Rydberg:

\[\frac{1}{\lambda} = R\left(\frac{1}{n_1^2} - \frac{1}{n_2^2}\right)\ \to\ \frac{1}{\lambda} = 1.097\cdot 10^7\ m^{-1}\left(\frac{1}{2^2} - \frac{1}{4^2}\right)\ \to\ \color[RGB]{0,112,192}{\bf{\frac{1}{\lambda} = 2.06\cdot 10^6\ m^{-1}}}\]

Como la velocidad de propagación es igual al producto de la longitud de onda por la frecuencia, si despejas el valor de la frecuencia:

\[c = \lambda\cdot \nu\ \to\ \nu = \color[RGB]{2,112,20}{\bf{c\cdot \frac{1}{\lambda}}}\]

Solo tienes que sustituir y calcular:

\[\nu = 3\cdot 10^8\ \cancel{m}\cdot s^{-1}\cdot 2.06\cdot 10^6\ \cancel{m^{-1}}\ \to\ \color[RGB]{192,0,0}{\boxed{\bf{\nu = 6.18\cdot 10^{14}\ s^{-1}}}}\]

Si lo necesitas, descarga en este enlace el archivo EDICO con la resolución de los problemas.

Creado con eXeLearning (Ventana nueva)