Tres ideas que cambiaron el mundo
A medida que se avanzaba en la técnica espectroscópica se obtenían registros más precisos y se pudo ver que algunas de las líneas de los espectros eran, en realidad, grupos de líneas muy próximas entre sí. También se conocía el «efecto Zeeman» (Peter Zeeman, 1896), por el que las líneas de un espectro se desdoblaban al someter la muestra a un campo magnético.
Este tipo de observaciones que no podían ser explicadas con el modelo de Bohr llevaron a su discípulo Arnold Sommerfeld a postular que las órbitas podían ser elípticas y, para ello, puso en juego otros dos parámetros además de «n». El problema esencial del modelo de Bohr y la corrección de Sommerfeld estaba en que mezclaban la mecánica clásica con postulados cuánticos.
Lo que llamamos mecánica cuántica nace en 1925 a partir de los trabajos que realizaron magníficos científicos como De Broglie, Dirac, Born, Heisenberg, Schrödinger, etc. Su fundamento está en la hipótesis de Planck y su punto de partida es la hipótesis de De Broglie.
Hipótesis de «de Broglie»
En la segunda mitad del siglo XVII existió una controversia bastante curiosa: dos científicos de la talla de Christiaan Huygens e Isaac Newton no se ponían de acuerdo en la naturaleza de la luz. Newton la consideraba como un conjunto de partículas (modelos corpuscular), mientras que Huygens estaba convencido de que se trataba de una onda (modelo ondulatorio).

|

|
Gracias a sus estudios sobre óptica, fue capaz de explicar fenómenos como la reflexión y la refracción de la luz a partir de la idea de que cada punto de un frente de ondas puede comportarse como una nueva fuente de ondas (principio de Huygens), aunque el renombre de Isaac Newton hizo que su modelo corpuscular se impusiera al modelo ondulatorio durante un siglo. A principios del siglo XIX, gracias a los experimentos de Thomas Young, la teoría ondulatoria fue demostrada y desbancó al modelo corpuscular de Newton.
Sin embargo, tal y como has visto, Einstein explicó el efecto fotoeléctrico en 1905 considerando la luz como un conjunto de partículas... ¿Querría esto decir que aquella controversia seguía sin resolución?

|
Esto es lo que se propuso el físico francés Louis-Victor Pierre Raymond de Broglie (1892 - 1987), conocido como Louis de Broglie, al plantearse la posibilidad de que existieran ondas de materia, del mismo modo que se había demostrado que la radiación tenía una partícula asociada; el fotón. Su intención era poder aunar ambos modelos para tener una explicación de los dos comportamientos observados en la luz. |
Consideró que la luz está compuesta por partículas y que la energía de estas debía estar cuantizada. Puedes entender cómo llegó a su ecuación de la longitud de onda de una partícula que se mueve si tienes en cuenta las ecuaciones para la energía de Planck y Einstein:
\[E = m\cdot c^2 \atop E = h\cdot \nu\]
Como la frecuencia puedes escribirla en función de la velocidad de propagación y la longitud de onda:
\[c = \lambda\cdot \nu\ \to\ \nu = \frac{c}{\lambda}\]
Igualando ambas expresiones de la energía y sustituyendo la frecuencia por su relación con la longitud de onda obtienes:
\[m\cdot c^2 = h\cdot \frac{c}{\lambda}\ \to\ \color[RGB]{2,112,20}\bf{\lambda = \frac{h}{m\cdot c}}\]
Si, en lugar de un fotón, aplicas esa expresión a una partícula másica que se mueva a una velocidad bastante menor que la velocidad de la luz:
\[\color[RGB]{192,0,0}\bf{\lambda = \frac{h}{m\cdot v}}\]

|
En esta imagen puedes ver la consecuencia gráfica de la ecuación anterior: un fotón lleva asociada una onda en su movimiento y la ecuación relaciona la masa y la velocidad del fotón con la longitud de onda de la onda asociada. |
|
Si en lugar de un fotón es una partícula másica, dado que el valor de la constante de Planck es muy pequeño, la masa ha de ser muy pequeña y la velocidad muy alta para poder percibir esa doble naturaleza. Esta dualidad es válida para partículas subatómicas que se mueven muy rápido. El registro de observaciones de la difracción de electrones en dos experimentos distintos, corroboró su hipótesis. En 1929 le fue otorgado el Premio Nobel de Física «por el descubrimiento de la naturaleza ondulatoria de los electrones». |

|

|
Este chiste gráfico puede ayudarte con la idea que debes recordar: Las cosas no «son», sino que «parecen». |
En 1927 se comprobó experimentalmente que los electrones, que son partículas materiales, presentan comportamiento ondulatorio en lo que se conoce como fenómeno de difracción de electrones.
Cuanto menor es el tamaño de la partícula que se mueve, más significativo es su comportamiento como onda. Del mismo modo, si la partícula es muy grande, su comportamiento corpuscular será mucho más significativo que su comportamiento como onda.
Esta conclusión abría la posibilidad de que los electrones del interior de los átomos pudieran ser observados como ondas.
Si lo necesitas, en este enlace puedes descargar la deducción matemática de De Broglie en formato EDICO.
Funciones de onda de Schrödinger
|
A partir de la hipótesis de la dualidad onda-corpúsculo, el físico austríaco Erwin Schrödinger (1887 - 1961) se decidió a describir al electrón del átomo de hidrógeno como la onda asociada a su movimiento en el interior del átomo. Para ello debía encontrar una ecuación que diese información sobre la energía y la posición del electrón, entendida por la zona en la que se podría mover en el interior del átomo. Esta idea la propuso en un modelo atómico ondulatorio no relativista, es decir, los electrones se caracterizan por sus ondas y se mueven a velocidades bastante menores que la velocidad de la luz. La función de onda funcionaba muy bien para explicar el átomo de hidrógeno e incluso el de helio, pero para átomos más grandes se obtenían valores incompatibles con el modelo. Sin embargo, la importancia de esta ecuación matemática es, para la física cuántica, como la segunda ley de Newton en la mecánica clásica. Se trata de un pilar fundamental del modelo mecano-cuántico. En 1933 le fue otorgado el Premio Nobel de física, junto a otro científico excepcional como fue Paul Dirac, «por el descubrimiento de nuevas formas productivas de la teoría atómica». |
.jpg)
|
¿Cómo es la función de onda?
La ecuación de Schrödinger es una ecuación diferencial que depende del tiempo y es muy compleja para describir sistemas reales, por eso se pueden hacer aproximaciones y obtener otras ecuaciones más simples que son aplicables a casos concretos, como es el caso de la ecuación para una partícula simple no relativista:
\[i\hbar \frac{\partial}{\partial t}\psi (r, t) = \left[\frac{-\hbar^2}{2\mu}\bigtriangledown^2 + V(r, t)\right]\psi (r, t)\]¡No te asustes! Es solo para que te hagas una idea de lo compleja que es la ecuación «simple».
La ecuación que nos interesa en Química es la ecuación para los estados estacionarios, es decir, su ecuación para sistemas independientes del tiempo. ¿Por qué? Porque, en ese caso, estaríamos ante ondas estacionarias descritas por medio de su función de onda y representando los «orbitales atómicos» y «moleculares».
La ecuación independiente del tiempo, de manera resumida, la podemos escribir como:
\[\color[RGB]{192,0,0}{\bf{\hat H\cdot \Psi = E\cdot \Psi}}\]Si aplicamos el operador hamiltoniano sobre una función de onda de un estado estacionario el resultado será proporcional a esa misma función de onda, siendo la constante de proporcionalidad la energía del propio estado estacionario.
Esto es muy importante porque nos permite relacionar los orbitales con los niveles de energía en el interior del átomo si lo aplicamos a los electrones.
¿Cómo se resuelve esa ecuación?
Como puedes imaginar, la resolución de la ecuación no es simple. El operador hamiltoniano que se aplica sobre la función de onda tiene la forma:
\[\hat H = \hat T + \hat V = -\frac{\hbar^2}{2\mu}\cdot \frac{\partial}{\partial x} + V(X)\](esto es solo para una dimensión)
Este operador es esencial en mecánica cuántica porque es el que nos permite conocer la energía asociada a la función de onda.
La ecuación diferencial de Schrödinger es continua, pero solo algunas soluciones son permitidas porque han de tener valores discretos; recuerda que la energía está cuantizada. Estas soluciones discretas se obtenían al aplicar restricciones matemáticas por medio de funciones propias, que contenían como parámetros a los «números cuánticos»
Se aplicó este tratamiento matemático al átomo de hidrógeno y se obtuvieron buenos resultados. También eran muy aceptables para el átomo de helio, lo que hizo que se adoptara como postulado teórico válido para partículas microscópicas. Sin embargo, al ser una función de onda estacionaria para partículas no relativistas, y en la que se despreciaba la interacción electromagnética, los resultados para átomos más grandes ya no eran satisfactorios.
En 1930, Max Born interpretó que la ecuación general de Schrödinger, sin las limitaciones dichas antes, tiene una componente de movimiento que podría ser una amplitud de probabilidad. Aplicó la mecánica cuántica matricial de Heisenberg a la resolución de la ecuación y obtuvo como solución zonas del espacio en las que había una gran probabilidad de encontrar a la partícula que se mueve. Esto le valió el Premio Nobel en 1954.
Wolfgang E. Pauli introdujo el espín electrónico en la ecuación de Schrödinger, para dar cuenta de los acoplamientos electrónicos y mejoró mucho los resultados obtenidos para otros átomos.
Más tarde, Paul Dirac, reformuló la ecuación para tener en cuenta también los efectos relativistas, convirtiendo la ecuación primigenia en una magnífica herramienta.
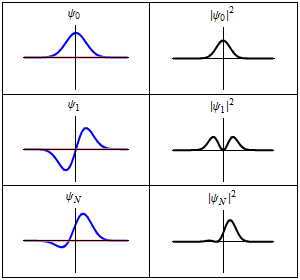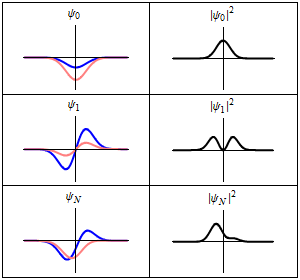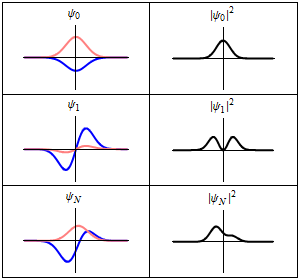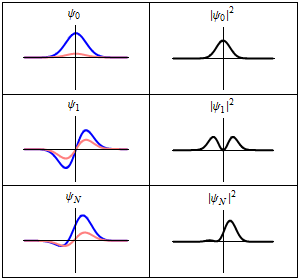
|
En la columna de la izquierda se muestran las funciones de onda y en la columna de la derecha se representan las distribuciones de probalibilidad. En las dos primeras filas se tienen sistemas estacionarios, mientras que en el última fila se muestra un estado no estacionario. |
|
|
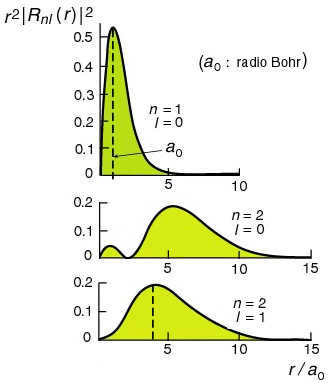
| A la izquierda puedes ver las soluciones encontradas para el cuadrado de la función de onda del átomo de hidrógeno y, a la derecha, la representación gráfica de esas soluciones. | |
Si lo necesitas, descarga en este enlace el desarrollo matemático de Schrödinger en formato EDICO.
¿Has oído hablar de la paradoja del gato de Schrödinger alguna vez? Se trata de una paradoja porque arranca con un experimento que no es posible llevar a la práctica y se llega a una solución que choca frontalmente con nuestra lógica. La paradoja conjuga todos los principios que has podido estudiar hasta ahora.
Te dejo aquí un vídeo que explica la paradoja del gato de Schrödinger, como manera de ilustrar que la mecánica cuántica implica probabilidades y no certezas:
Principio de indeterminación de Heisenberg

|
El físico alemán Werner Karl Heisenberg (1901 - 1976) tuvo una formación académica atípica y muy influenciada por los más brillantes físicos de la época. Su interés innato por las matemáticas lo llevó a plantearse el doctorado en «matemática pura» en 1920, aunque no pudo hacerlo con el profesor que eligió y este le recomendó que fuera el físico Sommerfeld quien lo supervisase. Se doctoró en 1923, aunque Sommerfeld tuvo sus dudas porque era un discípulo brillante en los aspectos teóricos, aunque muy poco habilidoso en la parte experimental. Fue compañero de estudios de Wolfgang Pauli. Acabado el doctorado, marcha a Gotinga y trabaja a las órdenes de Max Born. Un año después se marcha a Copenhague y trabaja con Bohr, pudiendo conocer a otros científicos excepcionales como Einstein. Como atesoraba un talento matemático excepcional, y tenía una tendencia natural a la física teórica, se propuso diseñar la manera de conseguir información de los electrones, pero sin tener en cuenta qué ocurría con ellos dentro de los átomos. Su idea era conocer el estado inicial y final del sistema y, por medio de cuadros de doble entrada, deducir qué había ocurrido en ese proceso, sin saber cómo había sido el proceso. Sin darse cuenta había inventado la «mecánica cuántica matricial». Fue Max Born quien se percató de que lo que hacía Heisenberg era aplicar la teoría de matrices. Fue galardonado con el Premio Nobel en 1932, poco antes de cumplir los 31 años, «por la creación de la mecánica cuántica, cuya aplicación tiene, entre otras cosas, el estudio y descubrimiento de las formas alotrópicas del hidrógeno». |
Como vas a aprender este curso, el producto de matrices no es conmutativo, es decir, no da el mismo resultado multiplicar A·B que B·A. Esta característica fue la que llevó a Heisenberg a enunciar su «Principio de indeterminación».
Este principio indica que, si queremos saber con precisión la información sobre dos «propiedades complementarias» de un sistema cuántico, no es posible lograrlo. Hay pares de magnitudes físicas que mantienen una dependencia intrínseca de manera que, si queremos precisar una de las magnitudes, la otra se hace más imprecisa y no es posible determinarla con exactitud. Heisenberg estableció dos pares de estas magnitudes: posición-momento lineal (x-p) y energía-tiempo (E-t).
\[\Delta x\cdot \Delta p \geq \dfrac{\hbar}{2} \geq \dfrac{h}{4\pi} \atop \Delta E\cdot \Delta t \geq \dfrac{\hbar}{2} \geq \dfrac{h}{4\pi}\]
Como puedes ver, ambos pares de magnitudes conjugadas tienen la misma indeterminación. Pero es necesario saber interpretar estas ecuaciones y ponerlas en contexto.
Pongamos en contexto esas ecuaciones
Como bien sabes, el valor de la constante de Planck es extremadamente pequeño, luego el cociente que aparece en el segundo término de la inecuación es del orden de 10-34. Esto quiere decir que solo podemos aplicar esta restricción a partículas y sistemas con valores de masa muy pequeños y velocidades considerables.
Imagina una mesa de billar en la que hay una bola. En cualquier momento podemos conocer la posición de la bola y su velocidad de manera precisa. Si está parada, sabríamos que su velocidad es cero y que su posición es una muy concreta, ¿verdad? Asumimos que al medir la masa y la posición de la bola siempre cometemos un error de precisión, pero cada vez podemos construir aparatos para medir con mayor precisión y esta «indeterminación» sería realmente despreciable. Supón que el error en la medición de la posición es de 0.5 cm y que el error en la medición de la velocidad, usando un velocímetro, es de 0.1 m/s, para una bola de 0.25 kg. ¿Cuál sería la indeterminación de nuestra medida? Basta con expresar ambas medidas en la misma unidad y hacer el cálculo:
\[5\cdot 10^{-3}\ m\cdot 0.25\ kg\cdot 10^{-1}\ \frac{m}{s} = \color[RGB]{192,0,0}{1.25\cdot 10^{-4}\ J\cdot s}\]Como puedes ver, el resultado es inmensamente mayor que la restricción impuesta por la inecuación de Heisenberg, por lo que siempre se va a cumplir y no tiene sentido aplicar el principio de indeterminación a sistemas macroscópicos.
Explicación para una partícula subatómica
En este vídeo puedes ver una explicación de este principio con un ejemplo de aplicación al caso de un electrón en el seno de un átomo:
Si lo necesitas, puedes descargar en este enlace el principio de Heisenberg y el contexto de las ecuaciones en formato EDICO.
La consecuencia de este principio es muy importante:
No podemos conocer el valor exacto de todas las magnitudes físicas que describen el estado de movimiento de las partículas.
La mecánica cuántica define «zonas de probabilidad» en la que encontrar a las partículas, estando estas zonas relacionadas con la energía de estas.