Su modelo estaba basado en los siguientes postulados:
1. Los electrones giran alrededor del núcleo en órbitas circulares en las que no emiten energía (órbitas estacionarias).
Impone este postulado para soslayar el hecho demostrado por Maxwell de que una carga eléctrica en movimiento emite energía. Las órbitas son circulares porque la fuerza centrípeta, debida a la velocidad con la que giran, es igual a la fuerza de atracción eléctrica entre el electrón y el núcleo:
K\cdot \frac{e^2}{r^2} = \frac{m_e\cdot v^2}{r}\ \to\ r = \frac{K\cdot e^2}{m_e\cdot v^2}
(K es la constante de Coulomb, e es la carga del electrón, me es la masa del electrón y v es la velocidad con la que gira el electrón en su órbita).
Se puede relacionar el radio de la órbita con la energía del electrón si tenemos en cuenta que la energía de éste será la suma de su energía cinética y su energía potencial: E = EC + EP.
E = \frac{1}{2}m_e\cdot v^2 - \frac{Ke^2}{r} = \frac{Ke^2}{2r} - \frac{Ke^2}{r} = \bf -\frac{Ke^2}{2r}
2. Las únicas órbitas posibles son aquellas en las que el momento angular del electrón es un múltiplo entero de h/2π.
Se trata de un postulado semiempírico porque esta condición la impone para que sea posible deducirse la ecuación empírica para la serie de Balmer (que proviene de la expresión de Rydberg).
m_e\cdot v\cdot r = n\cdot \hbar = n\cdot \frac{h}{2\pi}
Si despejamos v en la ecuación del primer postulado y la sustituimos en el segundo, obtenemos una ecuación que nos da el valor de los radios de las órbitas permitidas, en función del número n que ha de ser un número natural:
r = \frac{h^2}{4\pi^2\cdot K\cdot m_e\cdot e^2}\cdot n^2 = \bf a_0\cdot n^2
(siendo a0 la órbita de menor tamaño si n = 1)
| Si sustituimos los valores constantes que aparecen en la fracción obtenemos el valor 0,53 Å, lo que coincide con el radio de la primera órbita del átomo de hidrógeno (radio de Bohr). |
3. El electrón solo puede moverse entre órbitas permitidas de manera que emite o absorbe un fotón cuya energía viene dada por la expresión de Planck y que representa la diferencia de energía entre las órbitas inicial y final.
Como vimos en el primer enunciado, la energía total de un electrón vendrá dada por la suma de su energía cinética y su energía potencial. Si sustituimos el valor del radio obtenido en el segundo postulado en la expresión de la energía del electrón, obtendremos:
E = -\frac{Ke^2}{2r} = -\frac{Ke^2}{2\cdot\frac{h^2\cdot n^2}{4\pi^2\cdot K\cdot m_e\cdot e^2}} = -\frac{2\pi^2K^2e^4m_e}{h^2}\cdot \frac{1}{n^2}
Llamamos C a la parte constante de la ecuación y la frecuencia del fotón, a partir de la ecuación de Planck, quedaría como:
E = h\cdot \nu\ \to\ \nu = -\frac{C}{h}\cdot \frac{1}{n^2}
Como ese fotón es absorbido o emitido cuando el electrón cambia de órbita permitida, la variación de energía que experimenta el electrón vendría dada por la ecuación:
\nu = -\frac{C}{h}\cdot \left(\frac{1}{n_f^2} - \frac{1}{n_i^2}\right)
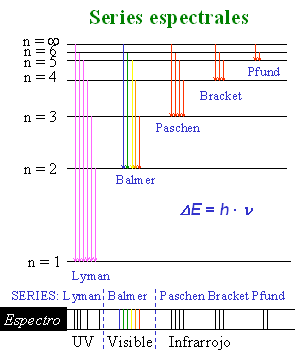
Esta expresión es muy similar a la ecuación de Rydberg y, dándole el valor nf = 2 se obtiene ¡¡la serie espectral de Balmer para el hidrógeno!!