|
Dado que el electrón dentro del átomo podía ser descrito como su onda asociada (De Broglie), el físico austríaco Erwing Schrödinger se propuso diseñar una función matemática que describiera al electrón del átomo de hidrógeno en función de sus propiedades ondulatorias. En 1926 publicó el desarrollo de su ecuación cuántica, lo que le valdría el Premio Nobel en 1933, compartido con Paul Dirac. Para que te hagas una idea de lo importante que es esta ecuación se dice que, en mecánica cuántica, es equivalente a la segunda ley de Newton en la mecánica clásica. |
.jpg)
|
4.3. Función de onda de Schrödinger
Breve resumen y contextualización
La ecuación de Schrödinger es una ecuación diferencial que depende del tiempo y es muy compleja para describir sistemas reales, por eso se pueden hacer aproximaciones y obtener otras ecuaciones más simples que son aplicables a casos concretos, como es el caso de la ecuación para una partícula simple no relativista:
i\hbar \frac{\partial}{\partial t}\psi (r, t) = \left[\frac{-\hbar^2}{2\mu}\bigtriangledown^2 + V(r, t)\right]\psi (r, t)
¡No te asustes! Es solo para que te hagas una idea de lo compleja que es la ecuación simple.
La ecuación que nos interesa en Química es la ecuación para los estados estacionarios, es decir, su ecuación para sistemas independientes del tiempo. ¿Por qué? Pues porque en ese caso estaríamos ante ondas estacionarias descritas por medio de su función de onda y representando los orbitales atómicos y moleculares.
La ecuación independiente del tiempo, de manera resumida, la podemos escribir como:
\hat H\cdot \psi = E\cdot \psi
Si aplicamos el operador hamiltoniano sobre una función de onda de un estado estacionario el resultado será proporcional a esa misma función de onda, siendo la constante de proporcionalidad LA ENERGÍA del propio estado estacionario.
Esto es muy importante porque nos permite relacionar los orbitales con los niveles de energía en el interior del átomo si lo aplicamos a los electrones.
Solución a la ecuación y modificaciones
Como puedes imaginar, la resolución de la ecuación no es simple. El operador hamiltoniano que se aplica sobre la función de onda tiene la forma:
\hat H = \hat T + \hat V = -\frac{\hbar^2}{2\mu}\cdot \frac{\partial}{\partial x} + V(X)
(esto es solo para una dimensión)
Este operador es esencial en mecánica cuántica porque es el que nos permite conocer la energía asociada a la función de onda.
La ecuación diferencial de Schrödinger es continua pero solo algunas soluciones son permitidas porque han de tener valores discretos (la energía está cuantizada). Estas soluciones discretas se obtenían al aplicar restricciones matemáticas por medio de funciones propias, que contenían como parámetros a los números cuánticos.
Se aplicó este tratamiento matemático al átomo de hidrógeno y se obtuvieron buenos resultados. También eran muy aceptables para el átomo de helio, lo que hizo que se adoptara como postulado teórico válido para partículas microscópicas. Sin embargo, al ser una función de onda estacionaria para partículas no relativistas, y en la que se despreciaba la interacción electromagnética, los resultados para átomos más grandes ya no eran satisfactorios.
En 1930, Max Born interpretó que la ecuación general de Schrödinger (sin las limitaciones dichas antes) tiene una componente de movimiento que podría ser una amplitud de probabilidad. Aplicó la mecánica cuántica matricial de Heisenberg a la resolución de la ecuación y obtuvo como solución zonas del espacio en las que había una gran probabilidad de encontrar a la partícula que se mueve. Esto le valió el Premio Nobel en 1954.
Wolfgang E. Pauli introdujo el espín electrónico en la ecuación de Schrödinger, para dar cuenta de los acoplamientos electrónicos y mejoró mucho los resultados obtenidos para otros átomos.
Más tarde, Paul Dirac, reformuló la ecuación para tener en cuenta también los efectos relativistas, convirtiendo la ecuación primigenia en una magnífica herramienta.
|
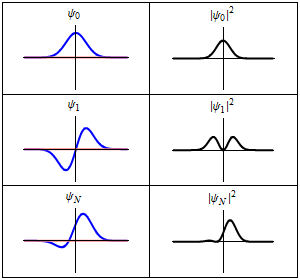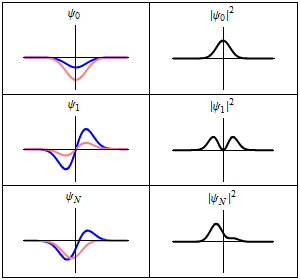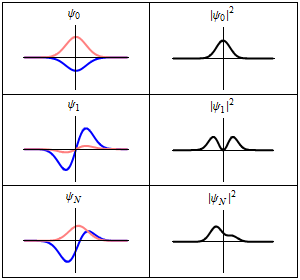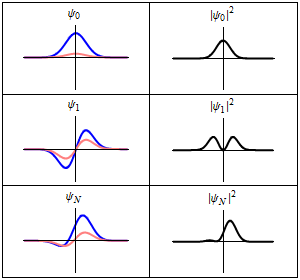
En la columna de la izquierda se muestran las funciones de onda y en la columna de la derecha se representan las distribuciones de probalibilidad. En las dos primeras filas se tienen sistemas estacionarios, mientras que en el última fila se muestra un estado no estacionario. |
Hablemos del gato de Schrödinger
¿Has oído hablar de la paradoja del gato de Schrödinger alguna vez?
Se trata de una paradoja porque arranca con un experimento que no es posible llevar a la práctica y se llega a una solución que choca frontalmente con nuestra lógica. La paradoja conjuga todos los principios que has podido estudiar hasta ahora.
Aquí puedes ver una explicación de esta paradoja:
Obra publicada con Licencia Creative Commons Reconocimiento Compartir igual 4.0