Cinemática, dinámica y estática

(#5462) Seleccionar

Volumen que emerge de un cubo de hierro que flota sobre mercurio (5462)

Un cubo de hierro de 4 cm de arista flota sobre mercurio. Suponiendo que la cara superior del cubo está en posición horizontal, calcula:

a) El volumen de hierro que emerge.

b) La longitud de la arista del cubo que sobresale de la superficie.

$\rho_{Fe} = 7.87\ g\cdot cm^{-3}$ ; $\rho_{Hg} = 13.9\ g\cdot cm^{-3}$
(#5370) Seleccionar

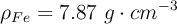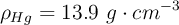
Diferencia de alcance en un lanzamiento parabólico con y sin rozamiento (5370)

Un objeto es lanzado con velocidad inicial 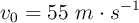$v_0 = 55\ m\cdot s^{-1}$ y ángulo con la horizontal de 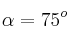$\alpha = 75^o$ . Calcula la diferencia aproximada entre el alcance en el modelo ideal y el alcance en el modelo con resistencia, suponiendo que b = 0.1.
(#5328) Seleccionar

Volumen de un cubo de aleación y masa de oro que contiene (5328)

Un cubo de aleación de aluminio y oro pesa 49 N. Al sumergirlo en agua suspendido de un dinamómetro la lectura del mismo es 39.2 N:

a) Calcula el volumen del cubo de aleación.

b) Calcula la masa de oro que contiene la aleación.

Datos: 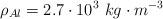$\rho_{Al} = 2.7\cdot 10^3\ kg\cdot m^{-3}$ ; $\rho_{Au} = 1.93\cdot 10^4\ kg\cdot m^{-3}$ ; $\rho_{H_2O} = 10^3\ kg\cdot m^{-3}$
(#5208) Seleccionar

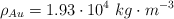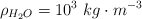
Variación de la densidad del agua con la profundidad (5208)

La densidad relativa del agua en la superficie del océano es de 1.025. Calcula:

a) La densidad del agua en el fondo, donde la presión es de 500 atmósferas.

b) El peso de un metro cúbico de agua a esa profundidad.

Datos: módulo de elasticidad del agua: 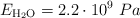$E_{\ce{H2O}} = 2.2\cdot 10^{9}\ Pa$ , densidad del agua pura: $\rho_{\ce{H2O}} = 10^3\ kg\cdot m^{-3}$ .
(#4778) Seleccionar

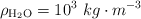Tiempo mínimo de un elevador en llegar a 40 ft de altura (4778)

Un elevador puede acelerar a 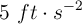$5\ ft\cdot s^{-2}$ y después desacelerar a 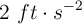$2\ ft\cdot s^{-2}$ . Determina el tiempo más corto que tardaría en llegar a un piso de una altura de 40 ft, sabiendo que ha de detenerse al llegar.